Б) Решение обратной геодезической задачи
Сущность решения задачи заключается в определении по прямоугольным координатам двух точек расстояния между ними и дирекционного угла направления с одной точки на другую ( рисунок 15 ).
Х
 |
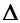 У
У
В
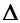 Х
Х 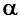 АВ d AB
АВ d AB 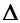 Х
Х
 |
А У

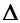 У
У
Рисунок 15 - Решение обратной геодезической задачи
Из треугольника АВС d2АВ = 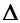 Х2 +
Х2 + 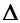 У2 . Из этого же треугольника следует, что если направление находится в первой четверти, то дирекционный угол ( АВ вычисляется из соотношения
У2 . Из этого же треугольника следует, что если направление находится в первой четверти, то дирекционный угол ( АВ вычисляется из соотношения
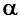 АВ = arc tg (±
АВ = arc tg (± 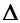 У ) / (± (
У ) / (± ( 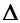 Х ).
Х ).
В общем случае для нахождения дирекционного угла направления необходимо определить румб направления по аналогичной формуле
rАВ = arc tg ( ± 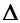 У ) / ( ±
У ) / ( ± 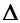 Х ),
Х ),
затем по знакам 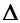 У и
У и 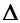 Х определить четверть, в которой находится направление, после чего перейти к дирекционному углу по соответствующей формуле таблицы 1.
Х определить четверть, в которой находится направление, после чего перейти к дирекционному углу по соответствующей формуле таблицы 1.
Вычислив румб r и дирекционный угол 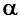 направления, расстояние d между двумя точками можно вычислить по формулам
направления, расстояние d между двумя точками можно вычислить по формулам



 d =
d = 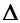 У / sin r =
У / sin r = 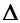 Х / cos r,
Х / cos r,
d = (± 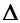 У ) / sin
У ) / sin 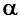 = ( ±
= ( ± 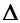 Х ) / cos
Х ) / cos  .
.