Спецификация переменных в уравнение регрессии. Ошибки спецификации.

 

Построение математической модели — это скорее искусство, чем наука, и, прежде всего, требует глубоких знаний предметной области. Социально-экономические системы имеют чрезвычайно сложную структуру, со многими явными и неявными взаимосвязями между эле­ментами системы, подвержены влиянию многих скрытых факторов, относятся к классу так называемых больших систем. Стечением време­ни меняются не только их характеристики, учитываемые в модели в виде отдельных параметров, но и структура самих уравнений, которые описывают процесс. Для их адекватного описания требуется соответст­вующий математический аппарат. Однако, даже самые сложные мате­матические методы не в состоянии описать реальную систему во всех ее деталях, да это и не нужно. Модель не должна быть слишком сложной. Излишняя детализация и учет второстепенных факторов затрудняет

исследование и не дает существенной информации об изучаемой системе. Если модель слишком сложна, то ее трудно использовать и интер­претировать на практике. Относительная простота — важная характе­ристика удачно построенной модели. С другой стороны, слишком уп­рощенная модель не будет адекватно описывать реальную систему. Таким образом, сложность модели должна соответствовать сложности изучаемого экономического объекта.

В связи с этим возникает необходимость формулировки некоторых разумных упрощающих гипотез (предположений), исключения из анализа второстепенных факторов и т. п., с тем, чтобы была возможность описать процесс математически. При этом существенные для данного социально-экономического процесса характерные черты должны быть учтены в модели в соответствии с поставленной целью исследования.

Другой характерной проблемой, с которой сталкивается эконометрист, является то, что часто приходится довольствоваться неточными данными, которые имеются в наличии и быстро устаревают. Этих дан­ных не всегда хватает, а провести управляемый эксперимент с целью получения дополнительной информации невозможно. В подобном случае целесообразно сочетание количественных методов с привлече­нием экспертных знаний и суждений.

В рамках эконометрического подхода существует мощный арсенал средств, который включает многие современные эффективные матема­тические методы, такие, например, как аппарат нейронных сетей, и разработанные на их основе компьютерные технологии, в известной степени помогающие справиться с этими проблемами. Но решающая роль принадлежит специалисту — эконометристу. Окончательный ус­пех зависит от его способности к неформальному анализу проблемной ситуации, адекватной оценке возможностей современных эконометрических методов, от их правильного применения и интерпретации полу­ченных результатов.

Построив удачную математическую модель и оценив ее количест­венно с использованием эконометрических методов, экономист-ана­литик получает в распоряжение эффективнейшее средство анализа и прогноза, а управляющий-практик — инструмент для обоснования управленческих решений. Такие модели широко применяются на практике.

 

Практически величина y складывается из двух слагаемых:

, где

- фактическое значение, результат признака;

- теоретическое значение результата признака, найденное из математической модели или уравнения регрессии;

- СВ, характерное отклонение реального значения результата признака от теоретического.

СВ называется возмущением. Она включает влияние неучтённых в модели факторов, случайных ошибок и особенно измерения. Её присутствие в модели порождено тремя источниками:

1) спецификацией модели;

2) выборочным характером исходных данных;

3) особенностями измерения.

От правильно выбранной спецификации модели зависит величина случайных ошибок: они тем меньше, чем больше теоретические значения результативного признака 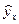подходит к фактическим данным y.

К ошибкам спецификации будут относиться не только неправильный выбор той или иной математической функции для 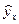, но и недоучет в уравнении регрессии какого-либо существенного фактора (например, использование парной регрессии вместо множественной).

Наряду с ошибками спецификации могут иметь место ошибки выборки (неоднородность данных в исходной статистической совокупности). Если совокупность неоднородна, то УР не имеет практического смысла.

Для получения хорошего результата обычно исключают из совокупности единицы с аномальными значениями исследуемых признаков, то есть результаты регрессии представляют собой выборочные характеристики.

Наибольшую опасность в практическом использовании методов регрессии представляют ошибки измерения. Если ошибки спецификации можно уменьшить, изменяя форму модели, а ошибки выборки – увеличивая объём исходных данных, то ошибки измерения практически сводят на нет все усилия по количественной оценке связи между признаками. Особенно велика роль ошибок измерения при исследовании на макроуровне.