Ранговая корреляция.
Метод линейной корреляции применяется для определения меры соответствия двух признаков, выраженных количественно, иными словами, - для численных величин. Это метод, который требует соответствия распределения данного исследуемого признака закону нормального распределения.
В отличие от этого метода, метод ранговой корреляции (корреляция Спирмена) применим к любым количественно измеренным или ранжированным данным. Этот метод способен, в отличие от других, измерять согласованность изменения разных признаков у одного испытуемого или выявлять совпадения индивидуальных ранговых показателей у двух испытуемых; или у испытуемого и усредненный показатель некой группы; или какие-либо показатели в сравнении двух групп.
Метод ранговой корреляции Спирмена позволяет определить силу и направление корреляционной связи между двумя признаками (или двумя иерархиями признаков).
Для подсчета ранговой корреляции необходимо располагать двумя рядами значений, которые могут быть проранжированы. Такими рядами могут быть:
А) Два признака, измеренные в одной и той же группе переменных (наиболее часто в этом качестве выступает группа людей, которых принято тогда именовать испытуемыми или респондентами. Естественно, под переменными подразумеваются не сами люди, а данные ими ответы на те или иные вопросы.)
Б) две индивидуальные иерархии признаков, выявленные у двух испытуемых по одному и тому же набору признаков (скажем, по ответам на пункты анкеты или теста).
В) Две групповые иерархии признаков (например, соответствие каких-либо выборов, сделанных одной группой людей выборам другой группы).
Г) Индивидуальная и групповая иерархии признаков (например, сопоставление индивидуальной иерархии жизненных ценностей сотрудника усредненному мнению группы на этот же счет; сопоставление последовательности товаров, которые приобрели бы (в среднем) жители города А и города Б при условии получения премии, на которую заранее не рассчитывали.)
Ограничения метода ранговой корреляции. По каждой переменной должно быть представлено не менее 5 наблюдений. Верхняя граница выборки – меньше или равна 40. Коэффициент ранговой корреляции Спирмена rs при большом количестве одинаковых рангов по одной или обеим сопоставляемым переменным дает огрубленные значения. В идеале оба коррелируемых ряда должны представлять собой две последовательности несовпадающих значений. В случае несоблюдения такого условия вносится поправка на одинаковые ранги (будет дано ниже). Помимо этих ограничений, следует так же помнить об ограничениях корреляционного метода вообще – невозможность обнаружения причинной связи между явлениями.
Алгоритм расчета ранговой корреляции.
1) Определить, какие два признака или две иерархии признаков будут участвовать в сопоставлении как переменные А и В.
2) Проранжировать значения переменной А, начисляя ранг 1 наименьшему значению, в соответствии с правилами ранжирования. Занести ранги во 2-й столбец таблицы по порядку номеров признаков. (В 1-м к тому моменту уже находятся номера или имена исследуемых признаков.)
3) Проранжировать значения переменной В и занести в 3-й столбец таблицы по порядку номеров.
4) Подсчитать разности d между рангами А и В по каждой строке и результаты занести в 4-й столбец таблицы.
5) Возвести каждую разность из столбца 4 в квадрат, и результаты занести в столбец №5.
6) Подсчитать сумму квадратов из столбца №5.
7) При наличии одинаковых рангов, рассчитать поправки: Тa =S(a3 – a)/12 и Тb =S(b3 – b)/12
Где a и b -= объем каждой группы рангов в соответствующем ранговом ряду А и В.
8) Рассчитать коэффициент ранговой корреляции rs при отсутствии одинаковых рангов – по формуле а; при наличии – по формуле б:
 Формула а: Формула б:
Формула а: Формула б:
rs = 1 – 6 (Sd2 + Тa + Тb) / N(N2 – 1)
Где: Sd2– квадратов разностей между рангами; Тa и Тb – поправки на одинаковые ранги;
N – количество признаков, участвовавших в ранжировании.
9) Определить по специальной таблице критические значения rs для данного N. Если rs превышает критическое значение или, по крайней мере, равен ему, - корреляция достоверно отличается от нуля.
При 0,05% уровне значимости:
| N (df=N-2) | Уровень значимости | |
| 0,05 (95%) | 0,01 (99%) | |
| 0,63 | 0,77 | |
| 0,44 | 0,56 |
Образец таблицы для внесения данных:
| Наименование признака | Ранги переменной А (по порядку) | Ранги переменной В (по порядку) | Разница между значениями двух предыдущих столбцов №2 и №3 | Квадрат значений предыдущего столбца №4 |
Формально (r-Пирсона): 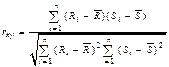 где R и S - ранги
где R и S - ранги
Преимущество r-Спирмена по сравнению с r-Пирсона — в большей чувствительности к связи в случае:
· существенного отклонения распределения хотя бы одной переменной от нормального вида (асимметрия, выбросы);
· криволинейной (монотонной) связи
Недостаток r-Спирмена по сравнению с r-Пирсона — в меньшей чувствительности к связи в случае несущественного отклонения распределения обеих переменных от нормального вида.
- Корреляция бинарных данных
Если обе переменные представлены в бинарной шкале (0,1), для изучения связи между ними можно применять φ-коэффициент сопряженности ( если для каждой переменной количество 0 и 1 приблизительно одинаковое).
Рассмотрим случай изучения связи двух бинарных переменных. Примеры таких переменных: пол (мужской, женский), образование (среднее, высшее), тревожность (низкая, высокая), успешность (низкая, высокая) и т. д. При изучении связей между бинарными переменными обычно строят четырехклеточные таблицы сопряженности:
| Признак X | Итог | |||
| Признак Y | а | b | a + b | |
| с | d | с + d | ||
| Итог | а + с | b + d | N |
В этом случае допустимо применение r-Пирсона непосредственно к исходным данным — двум бинарным переменным, принимающим значение 0 или 1, измеренным для каждого члена выборки численностью N. Результат применения r-Пирсона к двум бинарным переменным называется «фи-коэффициентом сопряженности» (Phi). Если данные представлены в четырехклеточной таблице сопряженности, то применяется формула, существенно упрощающая расчеты, но дающая аналогичный результат:

Пример. Исследовалась связь семейного положения студенток (X: 0 — холостая, 1 — замужем) и их академической успеваемости (Y: 0 — закончила вуз, 1 — отчислена).
| № | 2 | |||||||||||
| X | ||||||||||||
| У |
Таблица сопряженности для этих данных:
| X | Итог | |||
| У | ||||
| Итог |
Вычислим ср-коэффициент сопряженности:
 .
.
Получена умеренная положительная взаимосвязь: холостые студентки чаще заканчивают вуз, а замужние — чаше отчисляются. Отметим, что тот же самый результат был бы получен при применении формулы r-Пирсона непосредственно к исходным данным.
Итак, φ-коэффициент есть просто r-Пирсона, вычисленный для бинарных данных. Следовательно, интерпретация φ-коэффициента подобна интерпретации r--Пирсона. Но использование φ -коэффициента существенно ограничено. Чем больше асимметрия распределения 0 и 1 по каждой переменной, тем менее точно φ -коэффициент отражает связь между бинарными переменными. Иначе говоря, применение φ-коэффициента требует приблизительного равенства количества 0 u 1 no каждой переменной.