Пример 1 – Проверка статистических гипотез.

В мини исследовании на тему «Азарт и риск» принимало участие две группы испытуемых. В первую группу вошли 6 человек: любители азартных игр (экспериментальная группа). Во вторую группу вошли 8 случайным образом отобранных испытуемых (контрольная группа). Для оценки склонности человека к риску был разработан специальный опросник. Эмпирические данные представлены в таблице 1.1. Можно ли утверждать, что у любителей азартных игр склонность к риску выше, чем у группы случайным образом отобранных людей?

Таблица 1.1

Данные измерений показателя “склонность к риску”

 

I. Экспериментальная группа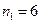
II. Контрольная группа

 

Рассчитаем средние значения склонности к риску в экспериментальной (I) и контрольной (II) группах:

;

.

Из полученных расчетов, видно, что выборочная средняя склонность к риску в экспериментальной группе азартных игроков ( 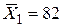) выше, чем и контрольной группе случайно отобранных людей ( ).

Можно ли утверждать, что полученные различия статистически значимы, не случайны?

Выберем критерий для проверки содержательной гипотезы о том, что у любителей азартных игр склонность к риску выше, чем у группы случайным образом отобранных людей.

Для проверки подобной гипотезы – о равенстве (различии) средних значений (уровней) признака в двух независимых выборках – предлагается несколько критериев [2], например:

- параметрический критерий Стьюдента сравнения средних;

- непараметрический критерий Розенбаума;

- непараметрический критерий Манна – Уитни.

Так как, каждая из независимых групп испытуемых представляет собой выборку малого объема, причем ( ), то для сравнения генеральных средних в данном случае наиболее корректным будет использование непараметрического критерия Манна – Уитни.

Сформулируем статистические гипотезы.

: различие двух групп испытуемых по уровню склонности к риску, является случайным (формально: );

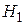: уровень показателя “склонность к риску” в экспериментальной группе азартных игроков статистически значимо выше, чем в контрольной группе случайно отобранных людей (формально: - случай направленных гипотез).

Для расчета эмпирического значения статистики критерия Манна – Уитни необходимо проранжировать данные наблюдений в двух группах испытуемых как единую выборку.

Процедура ранжирования осуществляется в два этапа:

1) упорядочение данных наблюдений, например, по возрастанию;

2) собственно ранжирование, т.е. приписывание упорядоченным данным порядковых номеров (рангов).

Дополнительно, осуществляется проверка правильности ранжирования: реальная сумма полученных рангов должна совпадать с расчетной теоретической, вычисляемой по формуле , где объем выборки.

Для удобства ранжирования и вычисления ранговых сумм в каждой группе составим расчетную таблицу (см. табл. 1.2).

Таблица 1.2