Для второй точки

ax₂ + b - y₂ = ε₂, и т.д.

Для последней точки

ax_n + b - y_n = ε_n.

Величины ε₁, ε₂, …, ε_n характеризуют отклонения рассматриваемых точек от точек искомой прямой: они выражают отклонения ординат точек наблюдения от ординат точек искомой прямой.

Метод наименьших квадратов требует подобрать значения параметров а и b таким образом, чтобы сумма квадратов отклонения ε_i, была при этом наименьшей, т.е.

Здесь x₁, x₂,..., x_n, y₁, y₂,..., y_n - заданные числа. Функция S есть функция двух независимых переменных a и b, т.е.:

S = f (a, b).

Необходимые условия существования экстремума функции дают:

¶S / ¶a = 0; ¶S / d¶b = 0.

Вычислим эти частные производные:

¶S / ¶a = 2 (ax₁ + b - y₁) x₁ + 2 (ax₂ + b - y₂) x₂ + ... +

+ 2 (ax_n + b - y_n) x_n,

¶S / ¶b = 2 (ax₁ + b - y₁) · 1 + 2 (ax₂ + b - y₂) · 1 + ... +

+ 2 (ax_n + b - y_n) · 1.

Приравнивая частные производные к нулю и сокращая на 2, получаем систему двух линейных уравнений с двумя неизвестными a и b:

(ax₁ + b - y₁) x₁ + (ax₂ + b - y₂) x₂ + ... + (ax_n + b - y_n) x_n = 0,

(ax₁ + b - y₁) + (ax₂ + b - y₂) + ... + (ax_n + b - y_n) = 0.

Раскрываем скобки, и после соответствующих преобразований получаем:

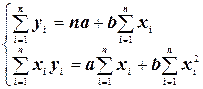(2.5)

Эти уравнения называются стандартными нормальными уравнениями, решение которых дает искомые значения a и b.

Система (2.5) может быть для удобства переписана следующим образом:

Такую систему, но без математического доказательства, мы уже рассматривали в курсе теории статистики.

Сущность метода наименьших квадратов может быть записана в наиболее общей форме в матричном виде:

E=Y-AX;

где Y – вектор фактических значений y;

AX – вектор расчетных значений y;

E – вектор остатков.

Решаем задачу на поиск экстремума:

Записываем в матричном виде дифференцирование и приравнивание к нулю:

 

 

Отсюда получаем общий вид системы нормальных уравнений для поиска параметров регрессионных моделей:

 

 

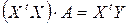
В данном выражении используются следующие обозначения:

- матрица значений факторных переменных.

 

m – число факторных переменных;

n – число их значений (статистических данных).

 

транспонированная матрица

 

Например, система уравнений для поиска параметров регрессионных моделей y=a₀ + a₁x₁ + a₂x₂ имеет вид:

 

 

Более подробно построение систем стандартных нормальных уравнений для двухфакторных уравнений множественной регрессии мы рассмотрим на следующих лекциях.

А сейчас мы рассмотрим теоретические предпосылки, которые положены в основу метода наименьших квадратов.

2й учебный вопрос. Сущность МНК и его теоретические предпосылки

Как мы уже отмечали раньше, сущность МНК сводится к поиску таких значений параметров некоторой математической функции, при которых достигает минимума сумма квадратов отклонений между фактическими и расчетными значениями зависимой переменной y.

В математической статистике доказывается, что при соблюдении определенных предпосылок о поведении так называемых «остатков» ε (т.е. отклонений расчетных значений от фактических) оценки параметров, полученные с помощью МНК, обладают некоторыми специальными свойствами (несмещенность, состоятельность и эффективность).

Несмещенность оценки означает, что математическое ожидание (средняя величина остатков) равна нулю, т.е. с ростом числа наблюдений остатки не будут накапливаться, и найденный параметр регрессии можно рассматривать как среднее значение из возможно большего количества оценок. Если оценки параметров обладают свойством несмещеннности, то их можно сравнивать по результатам разных исследований.

Для практических целей важна не только несмещенность, но и эффективность оценок. Оценки считаются эффективными, если они характеризуются минимальной дисперсией. В практических исследованиях это означает, что можно перейти от точечного оценивания к интервальному, то есть задать границы интервалов, в которых могут находиться наиболее вероятные значения «истинных» оценок параметров.

Если оценки параметров будут в дополнение к этим двум свойствам еще и состоятельными, то есть с увеличением объема выборки (числа наблюдений) точность оценок увеличивается (границы доверительных интервалов сужаются), то это обеспечивает реальную возможность использования построенных моделей в практических исследованиях, в частности, для проведения прогнозных расчетов.

Условия, необходимые для получения несмещенных, состоятельных и эффективных оценок параметров и представляют собой предпосылки метода наименьших квадратов (МНК), соблюдение которых желательно для получения надежных и достоверных результатов при расчетах по регрессионным моделям.

Предпосылки МНК соответствуют предположению о том, что имеется некая реальная статистическая зависимость между результативной переменной y и факторными переменными x1, x2, x3,…, которая описывается уравнением регрессии. Отклонения расчетных значений y от фактических (остатки) являются соответственно случайными величинами, подчиненными нормальному закону распределения (как большинство случайных величин в физическом мире).

После построения уравнения регрессии обычно проводится проверка наличия у случайных остатков ε тех свойств, которые предполагались, то есть проверяется выполнение следующих пяти предпосылок:

-случайный характер остатков

-нулевая средняя величина остатков, не зависящая от xi

-гомоскедастичность – то есть дисперсия каждого отклонения εi одинакова для всех значений х

-отсутствие автокорреляции остатков, то есть остатки распределены независимо друг от друга

-остатки подчиняются нормальному закону распределения.

Если не выполняется хотя бы одна из этих предпосылок, то нужно корректировать построенную модель.

Для проверки первой предпосылки обычно строится график зависимости остатков ε_i от теоретических значений результативного признака. Если на графике наблюдается горизонтальная полоса, то остатки носят случайный характер и применение МНК оправдано.

Вторая предпосылка означает, что Σε_i =0. Это обычно всегда выполняется для линейных моделей, но может быть нарушено при линеаризации нелинейных моделей.

Третья предпосылка: если это условие не соблюдается, то имеет место так называемая гетероскедастичность(дисперсия остатков растет по мере увеличения х или дисперсия остатков достигает максимальной величины при среднем значении переменной х и уменьшается при минимальном и максимальном значениях). Это обычно ведет к смещенности оценок параметров уравнений регрессии. Простейший способ проверки этой предпосылки – построение графика зависимости остатков от каждого из факторов х_j аналогично тому, как строится график для проверки первой предпосылки

Чтобы более строго оценить нарушение гомоскедастичности, можно также выполнить параметрический тест Голдфелда–Квандта, основные этапы которого заключаются в следующем:

1.Упорядочение n наблюдений по мере возрастания переменной х

2.Исключение из рассмотрения С центральных наблюдений, при этом (n-С):2>p, где р - число оцениваемых параметров

3.Разделение совокупности из (n-С) наблюдений на 2 группы (с малым и большим значением фактора х), и определение по каждой из групп уравнений регрессии

4.Определение остаточной суммы квадратов для 1-й (S1) и 2-й (S2) групп и нахождение их отношения: R=S1/S2.

Чем больше величина R превышает табличные значения F-критерия тем более нарушена предпосылка о равенстве дисперсий остаточных величин.

Четвертая предпосылка – это отсутствие автокорреляции, т.е. статистической зависимости (корреляции) между остатками текущих и предыдущих (последующих) наблюдений. Для проверки наличия или отсутствия автокорреляции рассчитывается коэффициент автокорреляции между ε_i и ε_j, где ε_j -остатки предыдущих наблюдений (j=i-1), который может быть определен как:

(2.6)

т.е. по обычной формуле линейного коэффициента корреляции между рядом значений остатков и этим же рядом, но сдвинутым на одно значение.

Если он окажется существенно отличен от нуля, то остатки автокоррелированы, и функция плотности вероятности зависит от jтой точки наблюдения и от распределения остатков в других точках наблюдения. Существует, кроме того, специальный критерий Дарбина-Уотсона для проверки наличия или отсутствия автокорреляции. Этот критерий рассчитывается по формуле:

d = Σ(ε_i- ε_i-1)²/ Σ ε²_i (2.7)

Легко проверить, что d≈2(1 – r₁), где r₁ – коэффициент автокорреляции первого порядка. Поэтому если при положительной автокорреляции r₁ ≈ 1, то d ≈ 0, и наоборот, а если автокорреляция отсутствует то r₁≈ 0, а d≈2.

При отрицательной автокорреляции r₁ ≈ -1, а d≈4

В целом для d выполняется неравенство 0≤ d ≤ 4

В эконометрике разработаны специальные таблицы критических значений (границ) для величины d, чтобы оценить допустимую степень близости этого критерия к 0 или к 4. Расчетное значение критерия Дарбина-Уотсона сравнивают с двумя табличными значениями d₁ и d₂ и делают следующие выводы:

Если d<d₁ , то гипотеза об отсутствии автокорреляции отвергается (с вероятностью 0,95).

Если d>d₂ , то гипотеза об отсутствии автокорреляции принимается с вероятностью 0,95.

Если d₁ ≤d ≤d₂ , то нет достаточных оснований для того, чтобы принять или отвергнуть гипотезу об отсутствии автокорреляции. Рекомендуется увеличить число переменных n.

Такая проверка осуществляется, если 0 ≤d <2. Если 2 <d ≤4 , то имеется так называемая отрицательная автокорреляция и с критическими значениями d₁ и d₂ сравнивается величина 4-d.

Более подробно критерий Дарбина-Уотсона рассматривается на лекции №6. Там же приводится таблица критических значений для величины d в зависимости от длины исходного ряда данных n и количества параметров уравнения регрессии m (табл.6.1).

Отсутствие автокорреляции остаточных величин обеспечивает состоятельность и эффективность оценок коэффициентов регрессии.

Проверка пятой предпосылки – гипотезы о нормальном распределении остатков может быть выполнена различными методами.

Во-первых, можно воспользоваться специальными статистическими критериями (Пирсона или Колмогорова), которые используются для проверки статистических гипотез о характере распределения случайных величин, но использование этих критериев требует достаточно трудоемких расчетов.

Во-вторых, можно рассчитать специальные показатели асимметрии и эксцесса по формулам (2.8) и (2.9):

Показатели асимметрии (А) и эксцесса (Э):

(2.8)

(2.9)

 

В случае если величина остатков распределена по нормальному закону, эти показатели должны быть близки к нулю. Чтобы оценить вероятность их близости к нулю (то есть проверить так называемую «нулевую» гипотезу) рассчитываются их среднеквадратические ошибки по формулам (2.10) и (2.11):

Среднеквадратические ошибки асимметрии (А) и эксцесса (Э):

σ _А = (2.10)

 

σ _Э = 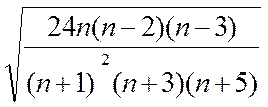(2.11)

Затем проверяется выполнение специальных условий (неравенств) условий, которые более подробно рассматриваются на лекции №6 «Линеаризация уравнений регрессии», так как необходимость проверки этих предпосылок чаще всего возникает в связи с построением нелинейных уравнений регрессии. Метод наименьших квадратов разработан для линейных уравнений. Его использование при расчете параметров нелинейных уравнений (после их приведения к линейному виду) может вызвать нарушение предпосылок МНК.

Иногда расчет показателей асимметрии и эксцесса не позволяет сделать точный вывод о нормальном характере распределения случайных величин.

В таких случаях для проверки нормального характера распределения требуется использование более мощных статистических критериев (например, критерия Пирсона или Колмогорова). Более подробно эти критерии будут рассмотрены на лекции №7.

3й учебный вопрос. Построение уравнения парной линейной регрессии

Рассмотрим содержание метода наименьших квадратов на конкретном примере построения уравнений парной линейной регрессии. Пусть имеются данные о сборе хлеба на душу населения по совокупности черноземных губерний. От каких факторов зависит величина этого сбора? Вероятно, определяющее влияние на величину сбора хлеба оказывает величина посева и уровень урожайности. Рассмотрим сначала зависимость величины сбора хлеба на душу населения (y) от показателя x₁, т.е. размера посевных площадей на душу (табл.2.1).

Таблица 2.1.