Условия Гаусса-Маркова

Для того чтобы регрессионный анализ, основанный на обычном методе наименьших квадратов, давал наилучшие из всех возможных результаты, случайная ошибка должна удовлетворять определенным условиям, известным как условия Гаусса-Маркова.

Понимание важности этих условий отличает компетентного исследователя от некомпетентного. Если условия не выполнены, надо это осознавать. А именно, если возможно, то провести корректирующие действия; если невозможно корректировка, то оценить, как невыполнение условий влияет на результат.

1-е условие Гаусса-Маркова состоит в том, что математическое ожидание случайной ошибки в любом наблюдении должно быть равно нулю:

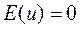
Это означает, что иногда случайная ошибка будет положительной, иногда отрицательной, но она не должна иметь систематического смещения. Фактически, если уравнение регрессии включает свободный член, то разумно предположить, что это условие выполнено автоматически, так как роль константы состоит в определении любой систематической тенденции объясняемой переменной, которую не учитывают объясняющие переменные, включенные в уравнение регрессии.

Таким образом, если уравнение регрессии включает постоянную 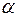, то именно константа содержит информацию о систематической тенденции в y. Поэтому 1-ое условие можно считать всегда выполненным.

В терминах зависимой переменной условие 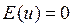означает, что 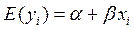,то есть при фиксированном х_i среднее значение y_i лежит на линии регрессии и равно .

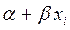2-е условие Гаусса-Маркова состоит в том, что дисперсия ошибки постоянна для всех наблюдений:

D(u_i) = s² = const, i = 1...n.

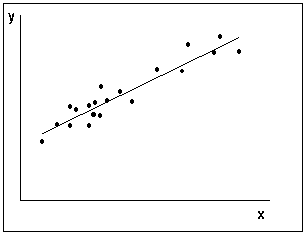
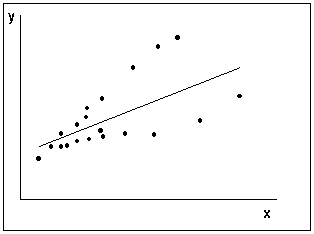
Условие независимости дисперсии от номера наблюдения называется гомоскедастичностью (homoscedasticity). Случай непостоянства дисперсии для разных наблюдений называется гетероскедастичностью (heteroscedasticity). На рис.5 а) приведен пример типичной картинки для случая гомоскедастичности ошибок, на рис. 5 б) – пример данных с гетероскедастичными ошибками.

 

а) гомоскедастичность ошибок	б) гетероскедастичность ошибок

Рисунок 4 – Принципиальные схемы случаев гомоскедастичности и гетероскедастичности ошибок

 

Иногда случайная ошибка будет больше, иногда меньше, однако не должно быть такого, что в одних наблюдениях ошибка систематически больше, чем в других. Эта постоянная дисперсия обозначается σ²_.

В терминах зависимой переменной условие гомоскедастичности формулируется как условие постоянства дисперсии y: D(y)=σ².

Если условие постоянства дисперсии не выполняется, то оценки, найденные по методу наименьших квадратов, будут неэффективны. Для получения более надежных результатов надо использовать модифицированный метод наименьших квадратов (см., например, Доугерти, 2001).

Величина σ² неизвестна. Одна из задач регрессионного анализа состоит в ее оценке, точнее оценке стандартного отклонения случайного члена.

3-е условие Гаусса-Маркова ‑ условие некоррелированности ошибок ‑ состоит в том, что предполагается отсутствие систематической связи между значениями случайной ошибки в любых двух наблюдениях:

cov(u_i, u_j) = 0, i ¹j.

Например, если случайная ошибка в одном наблюдении велика и положительна, то это не должно обусловливать систематическую тенденцию к тому, что в следующем наблюдении она будет обязательно мала и отрицательна (или велика и отрицательна, или мала и положительна). Случайные ошибки должны быть абсолютно независимы друг от друга, то есть ковариация между ними должна быть равна нулю.

Это условие часто нарушается в случае, когда наши данные являются временными рядами. В случае, когда условие некоррелированности ошибок не выполняется, то говорят об автокорреляции ошибок.

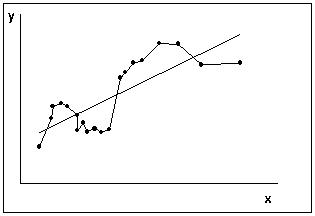
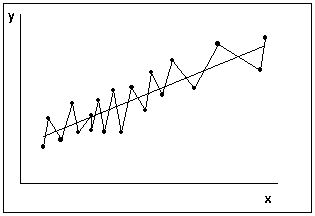
Типичная картинка автокорреляции ошибок представлена на рис. 6.

В терминах зависимой переменной условие отсутствия автокорреляции означает статистическую независимость значений y для разных наблюдений: cov(y_i, y_j)=0, i≠j.

Если третье условие не выполнено, то регрессия, оцененная методом наименьших квадратов, даст неэффективные результаты. Методы получения более надежных результатов представлены, например, в учебнике Кристофера Доугерти (2001).

 

а) ковариация ошибок положительна	б) ковариация ошибок отрицательна

Рисунок 5 – Принципиальные схемы автокорреляции ошибок

 

4-е условие Гаусса-Маркова – случайная ошибка должна быть распределена независимо от объясняющих переменных.

Значение объясняющей переменной x в каждом наблюдении должно считаться экзогенным, полностью определяемым внешними причинами, не учитываемыми в уравнении регрессии.

Во многих случаях используется более сильное условие: объясняющие переменные не являются стохастическими.

Предположение о нормальности распределения ошибок часто используется одновременно с условиями Гаусса-Маркова:

Ошибки u_i имеют совместное нормальное распределение с параметрами: математическое ожидание – 0, дисперсия – σ².

В терминах зависимой переменной условие нормальности распределения ошибок означает, что значения y также распределены по нормальному закону с параметрами: математическое ожидание – 0, дисперсия – σ².

При соблюдении перечисленных пяти условий регрессионная модель (41) называется классической нормальной линейной регрессионной моделью.

Итак, мы имеем набор данных (x_i,y_i) i=1…n, и классическую линейную регрессионную модель (выполняются четыре условия Гаусса-Маркова). Задача – оценить параметры модели α, β и дисперсию ошибки σ² «наилучшим» способом, то есть найти несмещенные эффективные состоятельные оценки.

Теорема Гаусса-Маркова

В предположениях классической линейной регрессии модели:

1) 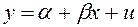‑ спецификация модели,

где x – неслучайная величина; y, u – случайные величины.

2)

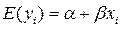
3)

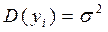
4)

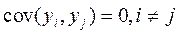
оценки а иb для параметров α и β, полученные по методу наименьших квадратов, имеют наименьшую дисперсию среди всех линейных несмещенных оценок, то есть аиb несмещенные эффективные оценки.

Таким образом, оценки аиb являются наилучшими в статистическом смысле.

 

4.6.3. Оценка дисперсии ошибок σ²

Имеем 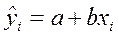‑ прогноз y_i в точке x_i.

Тогда . Здесь, как и прежде, e_i – остатки.

Не следует путать остатки e_i с ошибками u_i. Остатки тоже случайные величины, однако остатки e_i наблюдаемы в отличие от ошибок u_i.

Можно доказать, что - оценка дисперсии ошибок σ² определяется через сумму квадратов остатков по формуле:

(42)

Величина s² являются несмещенной оценкой дисперсии ошибок σ².

Квадратный корень из s² , то есть величина s называется стандартной ошибкой оценки .

 

4.6.4. Оценка дисперсий параметров модели a и b

.	(43)
.	(44)

 

Стандартное отклонение оценки коэффициента регрессии:

(45)