ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ
1. Кинетическая энергия электрона равна 1,02 МэВ. Вычислить длину волны де Бройля этого электрона.
Дано: Ek = 1,02 МэВ =16,2·10-14 Дж, E0 = 0,51 МэВ = 8,1·10-14 Дж.
Найти λ.
Решение. Длина волны де Бройля определяется по формуле  , (1) где λ — длина волны, соответствующая частице с импульсом
, (1) где λ — длина волны, соответствующая частице с импульсом  ;
; 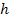 — постоянная Планка. По условию задачи кинетическая энергия электрона больше его энергии покоя: Еk = 2Е0, (2) следовательно, движущийся электрон является релятивистской частицей. Импульс релятивистских частиц определяется по формуле
— постоянная Планка. По условию задачи кинетическая энергия электрона больше его энергии покоя: Еk = 2Е0, (2) следовательно, движущийся электрон является релятивистской частицей. Импульс релятивистских частиц определяется по формуле
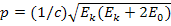 , (3)
, (3)
или, учитывая соотношение (2),
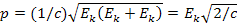 ; (4)
; (4)
Подставляя (4) в (1), получим
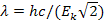 .
.
Производя вычисления, получим
 .
.
Ответ: λ = 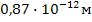 .
.
2. Используя соотношение неопределенностей Гейзенберга, показать, что ядра атомов не могут содержать электронов. Считать радиус ядра равным 10~18 см.
Дано: Rя = 10-15 м, 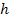 = 6,62·10-34 Дж·c.
= 6,62·10-34 Дж·c.
Решение. Соотношение неопределенностей Гейзенберга выражается формулой
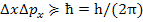 ;
;
где 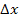 — неопределенность координаты;
— неопределенность координаты; 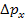 — неопределенность импульса;
— неопределенность импульса; 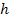 —постоянная Планка. Если неопределенность координаты принять равной радиусу ядра, т. е.
—постоянная Планка. Если неопределенность координаты принять равной радиусу ядра, т. е. 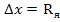 , то неопределенность импульса электрона выразим следующим образом:
, то неопределенность импульса электрона выразим следующим образом: 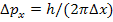 . Так как
. Так как 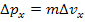 , то
, то 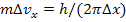 и
и 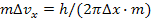 . Вычислим неопределенность скорости электрона:
. Вычислим неопределенность скорости электрона:
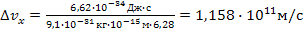 .
.
Сравнивая полученное значение 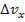 со скоростью света в вакууме с = 3·108 м/с, видим, что
со скоростью света в вакууме с = 3·108 м/с, видим, что 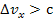 , а это невозможно, следовательно, ядра не могут содержать электронов.
, а это невозможно, следовательно, ядра не могут содержать электронов.
3. Электрон находится в бесконечно глубокой одномерной потенциальной яме шириной 1 нм в возбужденном состоянии. Определить минимальное значение энергии электрона и вероятность нахождения электрона в интервале 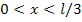 второго энергетического уровня.
второго энергетического уровня.
Дано: 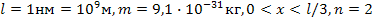 .
.
Найти: 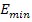 ,
,  .
.
В квантовой механике информацию о движении частиц получают из волновой функции (Т-функция), которая отражает распределение частиц или систем по квантовым состояниям. Эти частицы характеризуются дискретными значениями энергии, импульса, момента импульса; т. е. 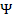 - функция является функцией состояния частиц в микромире. Решая уравнение Шредингера, получим, что для рассматриваемого случая собственная функция имеет вид
- функция является функцией состояния частиц в микромире. Решая уравнение Шредингера, получим, что для рассматриваемого случая собственная функция имеет вид
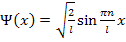 , (1)
, (1)

где 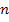 = 1, 2, 3, ...;
= 1, 2, 3, ...;  — координата частицы;
— координата частицы;  — ширина ямы. Графики собственных функций изображены на рис. 17. Согласно соотношению де Бройля двум отличающимся знаком проекциям импульса соответствуют две плоские монохроматические волны де Бройля, распространяющиеся в противоположных направлениях вдоль оси
— ширина ямы. Графики собственных функций изображены на рис. 17. Согласно соотношению де Бройля двум отличающимся знаком проекциям импульса соответствуют две плоские монохроматические волны де Бройля, распространяющиеся в противоположных направлениях вдоль оси  . В результате их интерференции возникают стоячие волны де Бройля, характеризующиеся стационарным распределением вдоль оси
. В результате их интерференции возникают стоячие волны де Бройля, характеризующиеся стационарным распределением вдоль оси  амплитуды колебаний. Эта амплитуда и есть волновая функция
амплитуды колебаний. Эта амплитуда и есть волновая функция 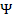 (х), квадрат которой определяет плотность вероятности пребывания электрона в точке с координатой
(х), квадрат которой определяет плотность вероятности пребывания электрона в точке с координатой  . Как видно из рис. 17, для значения
. Как видно из рис. 17, для значения 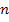 =1 на ширине ямы
=1 на ширине ямы  укладывается половина длины стоячей волны де Бройля, для
укладывается половина длины стоячей волны де Бройля, для 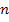 =2 — целая длина стоячей волны де Бройля и т. д., т. е. в потенциальной яме могут быть лишь волны де Бройля, длина которых удовлетворяет условию
=2 — целая длина стоячей волны де Бройля и т. д., т. е. в потенциальной яме могут быть лишь волны де Бройля, длина которых удовлетворяет условию
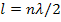 (
(  )
)
Таким образом, на ширине  ямы должно укладываться целое число полуволн:
ямы должно укладываться целое число полуволн: 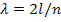 . (2)
. (2)
Полная энергия частицы в потенциальной яме зависит от ее ширины  и определяется формулой
и определяется формулой 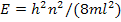 , (3) где
, (3) где 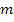 — масса частицы;
— масса частицы; 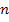 - 1, 2, 3... . Минимальное значение энергии электрон будет иметь при минимальном значении
- 1, 2, 3... . Минимальное значение энергии электрон будет иметь при минимальном значении 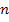 , т.е. при
, т.е. при 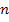 =1. Следовательно,
=1. Следовательно,
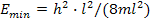 .
.
Подставляя числовые значения, получим
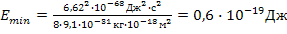 .
.
Вероятность того, что электрон будет обнаружен в интервале от  до
до 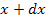 , равна
, равна 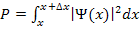 . Искомую вероятность находим интегрированием в пределах от 0 до
. Искомую вероятность находим интегрированием в пределах от 0 до 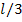 :
:
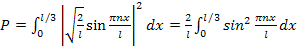 .
.
Используя соотношение  , вычисляем интеграл при условии, что электрон находится на втором энергетическом уровне:
, вычисляем интеграл при условии, что электрон находится на втором энергетическом уровне:
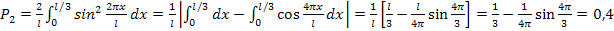 ;
;
Ответ:  ,
, 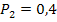
4. Граничная длина волны Кα - серии характеристического рентгеновского излучения для некоторого элемента равна 0,0205 нм. Определить этот элемент.
Дано: 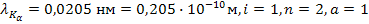 .
.
Найти Z.
Решение. Из формулы Мозли
 ,
,
где λ — длина волны характеристического излучения, равная 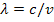 (с — скорость света, v — частота, соответствующая длине волны λ); R — постоянная Ридберга; Z — порядковый номер элемента, из которого изготовлен электрод;
(с — скорость света, v — частота, соответствующая длине волны λ); R — постоянная Ридберга; Z — порядковый номер элемента, из которого изготовлен электрод; 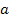 — постоянная экранирования;
— постоянная экранирования;  — номер энергетического уровня, на который переходит электрон;
— номер энергетического уровня, на который переходит электрон; 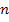 — номер энергетического' уровня, с которого переходит электрон (для Кα - серии
— номер энергетического' уровня, с которого переходит электрон (для Кα - серии  =1,
=1, 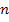 =2,
=2, 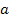 =1), находим Z:
=1), находим Z:
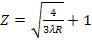 ;
;
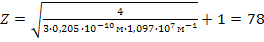 .
.
Порядковый номер 78 имеет платина.
Ответ: Z = 78 (платина).
5. На поверхность воды падает узкий монохроматический пучок γ-лучей с длиной волны 0,775 пм. На какой глубине интенсивность γ-лучей уменьшится в 100 раз!
Дано: λ = 0,775 пм = 7,75·10-13 м,  =100.
=100.
Найти 
Решение. Ослабление интенсивности γ-лучей определяется из формулы 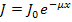 , (1) откуда
, (1) откуда 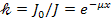 , где
, где  — интенсивность падающего пучка γ-лучей;
— интенсивность падающего пучка γ-лучей;  — их интенсивность на глубине
— их интенсивность на глубине  ;
; 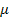 — коэффициент линейного ослабления. Решая уравнение (1) относительно
— коэффициент линейного ослабления. Решая уравнение (1) относительно  , находим
, находим
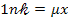 ;
; 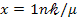 . (2)
. (2)
Для определения 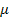 , вычислим энергию γ-квантов
, вычислим энергию γ-квантов  , где
, где 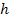 — постоянная Планка; с — скорость света в вакууме. Подставляя числовые значения, получим
— постоянная Планка; с — скорость света в вакууме. Подставляя числовые значения, получим
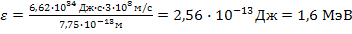 .
.
По графику зависимости линейного коэффициента ослабления γ-лучей от их энергии (рис. 18) находим 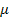 = 0,06 см-1. Подставляя это значение ц в формулу (2), находим
= 0,06 см-1. Подставляя это значение ц в формулу (2), находим
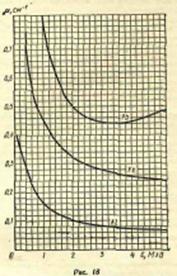
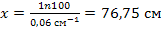 .
.
Ответ: 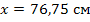
6. Определить, сколько ядер в 1 г радиоактивного 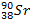 распадается в течение одного года.
распадается в течение одного года.
Дано: 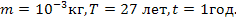
Найти 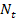
Решение. Для определения числа атомов, содержащихся в 1 г 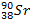 , используем соотношение
, используем соотношение
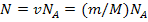 ,
,
где  – постоянная Авогадро;
– постоянная Авогадро;  - число молей, содержащихся в массе данного элемента; M - молярная масса изотопа. Между молярной массой изотопа и его относительной атомной массой существует соотношение: М = 10-3 А кг/моль. (2) Для всякого изотопа относительная атомная масса весьма близка к его массовому числу А, т. е. для данного случая M = 10-3·90 кг/моль = 9·10-2 кг/моль.
- число молей, содержащихся в массе данного элемента; M - молярная масса изотопа. Между молярной массой изотопа и его относительной атомной массой существует соотношение: М = 10-3 А кг/моль. (2) Для всякого изотопа относительная атомная масса весьма близка к его массовому числу А, т. е. для данного случая M = 10-3·90 кг/моль = 9·10-2 кг/моль.
Используя закон радиоактивного распада
 , (3)
, (3)
где 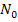 — начальное число нераспавшихся ядер в момент
— начальное число нераспавшихся ядер в момент 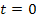 ; N — число нераспавшихся ядер в момент
; N — число нераспавшихся ядер в момент  ; λ — постоянная радиоактивного распада, определим количество распавшихся ядер
; λ — постоянная радиоактивного распада, определим количество распавшихся ядер 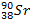 в течение 1 года:
в течение 1 года:
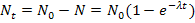 . (4)
. (4)
Учитывая, что постоянная радиоактивного распада связана с периодом полураспада соотношением λ = 1n 2/T, получим
 . (5)
. (5)
Подставляя (1) с учетом (2) в выражение (5), имеем
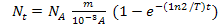 . (6)
. (6)
Произведя вычисления по формуле (6), найдем
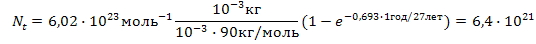
Ответ: 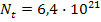
7. Вычислить в мегаэлектрон-вольтах энергию ядерной реакции:

Выделяется или поглощается энергия при этой реакции?
Решение. Энергию ядерной реакции  , (1), где
, (1), где 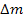 — дефект массы реакции; с — скорость света в вакууме. Если
— дефект массы реакции; с — скорость света в вакууме. Если 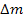 выражать в а.е.м., то формула (1) примет вид
выражать в а.е.м., то формула (1) примет вид  . Дефект массы равен
. Дефект массы равен
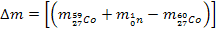 .
.
Так как число электронов до и после реакции сохраняется, то вместо значений масс ядер воспользуемся значениями масс нейтральных атомов, которые приводятся в справочных таблицах:
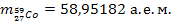 ;
; 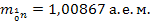 ;
; 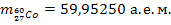 ;
;
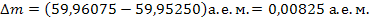
Реакция идет с выделением энергии, так как 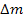 >0:
>0:
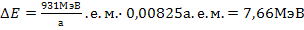
Ответ: 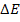 =7,66 МэВ.
=7,66 МэВ.
8. Медь имеет гранецентрированную кубическую решетку. Расстояние между ближайшими атомами меди 0,255 нм. Определить плотность меди и параметр решетки.
Дано: d = 0,255 нм = 2,55·10-10 м, 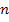 =4, М=бЗ,54·10-3 кг/моль.
=4, М=бЗ,54·10-3 кг/моль.
Найти: р, а.
Решение. Плотность кристалла меди найдем по формуле  , (1) где М — молярная масса меди;
, (1) где М — молярная масса меди; 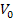 — молярный объем. Он равен объему одной элементарной ячейки
— молярный объем. Он равен объему одной элементарной ячейки 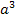 , умноженной на число
, умноженной на число 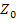 элементарных ячеек, содержащихся в одном моле кристалла:
элементарных ячеек, содержащихся в одном моле кристалла:  . (2)
. (2)
Число элементарных ячеек, содержащихся в одном моле кристалла, состоящего из одинаковых атомов, найдем, разделив постоянную Авогадро  на число
на число 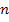 атомов, приходящихся на одну элементарную ячейку:
атомов, приходящихся на одну элементарную ячейку:  . (3) Для кубической гранецентрированной решетки
. (3) Для кубической гранецентрированной решетки 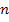 = 4. Подставляя (3) в (2), получим
= 4. Подставляя (3) в (2), получим
 . (4)
. (4)
Подставляя (4) в (1), окончательно имеем
 .
.
Расстояние между ближайшими соседними атомами связано "с параметром решетки а простым геометрическим соотношением (рис. 19):
 .
.
Подставляя числовые значения в расчетные формулы, находим
 ;
;
 .
.
Ответ:  ;
;  .
.

Рис. 19
9. Кристаллический алюминий массой 10 г нагревается от 10 до 20 К. Пользуясь теорией Дебая, определить количество теплоты, необходимое для нагревания. Характеристическая температура Дебая для алюминия равна 418 К. Считать, что условие Т 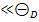 выполняется.
выполняется.
Дано: 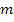 = 0,01 кг,
= 0,01 кг,  = 10 К,
= 10 К,  = 20 К,
= 20 К,  =418 К,
=418 К,  = 27·10-3 кг/моль.
= 27·10-3 кг/моль.
Найти Q.
Решение. Количество теплоты, необходимое для нагревания алюминия от температуры  до
до  , будем вычислять по формуле
, будем вычислять по формуле
 (1)
(1)
где 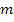 — масса алюминия; с — его удельная теплоемкость, которая связана с молярной теплоемкостью соотношением
— масса алюминия; с — его удельная теплоемкость, которая связана с молярной теплоемкостью соотношением  . Учитывая это, формулу (1) запишем в виде
. Учитывая это, формулу (1) запишем в виде
 (2)
(2)
По теории Дебая, если условие Т 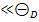 выполнено, молярная теплоемкость определяется предельным законом
выполнено, молярная теплоемкость определяется предельным законом
 ,
,
где R = 8,31 Дж/(моль·К) — молярная газовая постоянная;  — характеристическая температура Дебая; Т — термодинамическая температура. Подставляя (3) в (2) и выполняя интегрирование, получаем
— характеристическая температура Дебая; Т — термодинамическая температура. Подставляя (3) в (2) и выполняя интегрирование, получаем
 .
.
Подставляя числовые значения, находим

Ответ:  = 0,36 Дж.
= 0,36 Дж.