Основные законы и формулы

 

Скорость мгновенная

υ= или υ=

Ускорение:

 

мгновенное

a= =

тангенциальное

a_τ= =

нормальное

a_n=

полное

a=

Скорость угловая

То же, для равномерного вращательного движения

ω =const; ω =φ/t; 2π/T=2πυ

Ускорение угловое

Уравнения равнопеременного вращательного движения

/2

Связь между линейными и угловыми величинами,

характе­ризующими движение точки по окружности

s=φr; υ=ωr; a_τ=εr

a_n=ω²r

Второй закон Ньютона для поступательного движения

Сила, действующая на тело массы m (m=const)

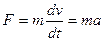
Количество движения мате­риальной точки массы т,

дви­жущейся со скоростью v

p=mv

 

Сила, действующая на тело,

движущееся по окружности радиуса r

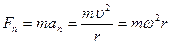
Закон сохранения количества движения

для изолированной системы

Сила трения (скольжения)

F_тр=fF_n (здесь F_n-сила нормального давления)

Скорости шаров массами m₁ и m₂

после абсолютно упругого центрального удара

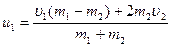
Скорость шаров массами m₁ m₂

после абсолютного неуп­ругого удара

Работа переменной силы на пути s

Мощность

;

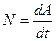Сила упругости

А= -kx

 

Сила гравитационного вза­имодействия

F=Gm₁m₂/r²

Потенциальная энергия:

упругодеформированного тела (работа упругой си­лы)

 

П=A=kx²/2

гравитационного взаимо­действия тела,

находящего­ся в однородном поле тя­жести

П=-Gm₁m₂/r

П=mgh

(g-ускорение свободного падения)

Кинетическая энергия тела

;

Закон сохранения механиче­ской энергии

 

E=T+П=const

 

 

Напряженность гравитацион­ного поля Земли

Потенциал гравитационного поля Земли

Момент инерции материаль­ной точки

J=mr²

Моменты инерции некоторых тел массой т:

полого и сплошного ци­линдров (или диска)

ра­диуса R относительно оси вращения,

совпадающей с осью цилиндра

J_п.ц=mR²; J_спл=mR²/2

шара радиуса Rотноси­тельно оси вращения,

про­ходящей через центр масс шара

J₀=0,4mR²

тонкого стержня длиной l,

если ось вращения перпен­дикулярна стержня

и про­ходит через центр масс стержня

то же, но ось вращения проходит через

один из концов стержня

тела относительно

произ­вольной оси (теорема Штейнера)

Момент силы относительно оси вращения

M=F_r

 

Основное уравнение динами­ки вращательного движения

То же, при J = const

Закон сохранения момента количества

движения для изо­лированной системы

Кинетическая энергия вра­щающегося тела

/2

Работа при вращательном движении

 

Энергия покоя частицы

Теорема сложения скоростей в теории относительности

Зависимость массы частицы от скорости V,

сравнимой со скоростью света

 

 

Полная энергия частицы, движущейся со скоростью υ,

сравнимой со скоростью света

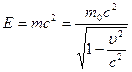
Кинетическая энергия реля­тивистской частицы

Зависимость длины тела и

времени от скорости в реляти-

вистской механике