Билет 7. ФСР однородной системы уравнений. Теорема о существовании ФСР.

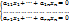(1)

 

Определение. Пусть n- число неизвестных, r = Rg A однородной системы ЛАУ. Фундаментальным решением системы называется любая линейно независимая система из n-r решений.

Если Rg A = n, то система имеет только нулевое решение. Пусть r = Rg A < n. Тогда в А существует базисный минор порядка r. Не ограничивая общности считаем базисным минором 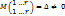.Строки а₁, …, а_{r —} базисные.

По теореме о базисном миноре строки a_r+1, …, a_n линейно выражаются через базисные, т.е.. все уравнения системы являются линейными комбинациями первых r уравнений. (2) Система (2) эквивалентна (1) Назовем неизвестные x₁, …, x_r – главными неизвестными, а x_r+1, …, x_n – свободные неизвестные. (4) Система (4) эквивалентна системе (2) Т.к.. 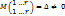, поэтому при заданных значениях свободных неизвестных главная неизвестная определяется однозначно. (По теореме Крамера.)

Теорема 7. Если r = Rg A < n, то система (1) однородной системы ЛАУ имеет n-r линейно независимых решений.

Доказательство. 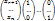– свободные неизвестные. – линейно независимы. Rg( ) = n-r

=

 

 

8.Линейная зависимость любых (n-r+1) решений однородной системы. Общее решение однородной системы ЛАУ.

Теорема1: если r = RgA < n, то любая система из (n-r+1) решений однородной системы линейно зависима.

Доказательство: рассмотрим произвольные (n-r+1) решения однородной системы ЛАУ:

= …… = , =

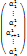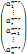Создадим матрицу B: , RgB ≤ n-r < n-r+1 =>столбцы B линейно зависимы

= > существуют такие , …, , 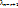(не все равные нулю), что будет выполнятся:

+ … + + = ; = + … + = ;

 

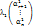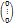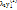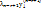- решение однородной системы ЛАУ(по критерию существования ненулевых решений)

Итак, существуют такие , …, , 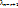(не все равные нулю), что + … + =

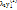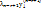Теорема 2: если r=RgA < n и 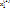, …, 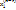– ФСР однородной системы ЛАУ, то общее решение системы имеет вид: = 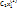+ … + 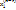, где , …, - произвольные числа