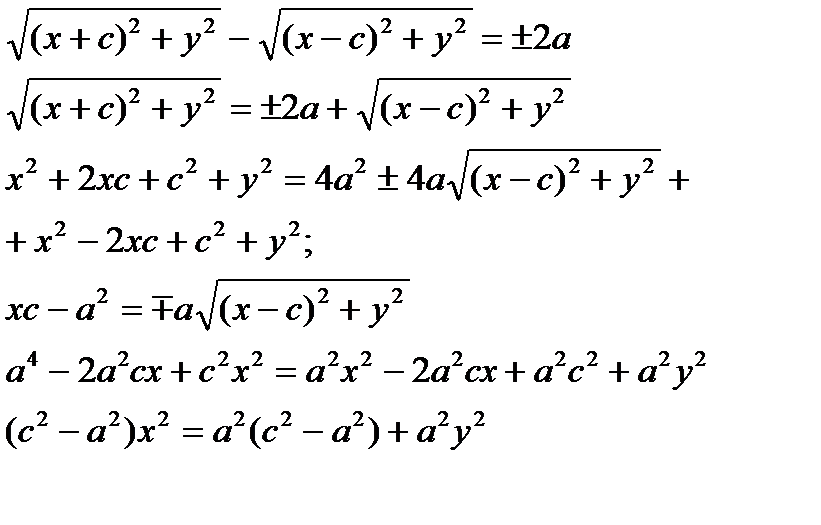Эллипс. Определение. Вывод канонического уравнения.

y M (x;y)     F1 (-c;0) O F2 (c;0) x

Эллипсомназывается

геометрическое место всех

точек плоскости, сумма

расстояний от которых до

до фокусов есть величина

постоянная, большая, чем расстояние между фокусами.

Пусть М (х;у) – произвольная точка эллипса.

Т.к. MF₁ + MF₂ = 2a

Т.к.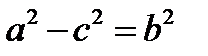

То получаем

Или

 

Гипербола. Определение. Вывод канонического уравнения.

Гиперболойназывается множество всех точек плоскости, модуль разности расстояний от каждой из которых до фокусов есть величина постоянная.

Пусть M(x;y) – произвольная точка гиперболы. Тогда согласно определению гиперболы |MF₁ – MF₂|=2a или MF₁ – MF₂=±2a,