ЗАДАНИЕ 3
В задании предлагается решить задачи по теме: "Элементы финансовой математики в экономике недвижимости".
Вся методология оценки недвижимости построена на аксиоме "деньги завтра не есть деньги сегодня". Основными операциями, позволяющими сопоставлять разновремённые деньги, являются операции накопления и дисконтирования.
Накопление это процесс определения будущей стоимости денег FV (Future Value – будущая стоимость).
Дисконтирование это процесс приведения денежных поступлений к текущей стоимости PV (Present Value – текущая стоимость).
При операциях приведения денежных поступлений к их будущей стоимости ставку процента принято называть ставкой дохода.
При операциях приведения денежных поступлений к их текущей стоимости ставку процента принято называть ставкой дисконта.

|
|
 |
Дисконтирование (по ставке дохода – i)
Использование сложного процента предполагает начисление процентов на сумму первоначального вклада и начисленных за предыдущие периоды процентов. То есть полученный процент вместе с первоначальными инвестициями становится частью основной суммы. Использование простого процента предполагает начисление процентов в течение всех периодов на первоначальную сумму. То есть не начисляются проценты на проценты.
Будущая стоимость денежной единицы (накопленная сумма денежной единицы) – показывает рост стоимости денежной единицы, положенной на депозит с начислением процентов на сумму вклада и ранее начисленные проценты:
FV = PV (1 + i)n, (1)
где FV – будущая стоимость денег;
PV – текущая стоимость денег;
i – процентная ставки (ставка дохода);
n –число лет.
Фактор показывает, какая сумма будет накоплена на счёте к концу определенного периода при заданной ставке дохода, если сегодня положить на счёт 1 денежную единицу.
Правило 72. Для примерного определения срока удвоения капитала в годах необходимо 72 разделить на целочисленное значение годовой ставки дохода на капитал. Правило применимо для ставок дохода на капитал в интервале 3 – 18 %.
Текущая стоимость денежной единицы (реверсия) – показывает текущую стоимость одной денежной единицы будущего единовременного поступления с учётом заданного процента. При заданной ставке дисконта даёт оценку текущей стоимости того денежного потока, который может быть получен (заплачен) в конце определённого периода:
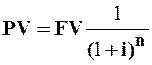 . (2)
. (2)
Фактор показывает, какова при заданной ставке дисконта текущая стоимость одной денежной единицы, получаемой в конце определенного периода времени.
Текущая стоимость аннуитета
Аннуитет (далее обозначается РМТ) – это серия равновеликих платежей или поступлений, отстоящих друг от друга на один и тот же промежуток времени.
Аннуитеты бывают авансовые и обычные. Авансовый аннуитет это периодические платежи, поступающие в начале периода начисления процентов (здесь не рассматривается).
Обычный аннуитет показывает текущую стоимость равномерного потока доходов или постоянного ряда равных платежей, когда все поступления происходят в конце периода:
 . (3)
. (3)
Фактор показывает, какова при заданной ставке дисконта текущая стоимость серии платежей в одну денежную единицу в течение определенного периода.
Будущая стоимость аннуитета (накопление единицы за период) показывает будущую стоимость ряда равных платежей, поступлений размером в одну денежную единицу при заданной ставке и сроке:
 . (4)
. (4)
Данная функция на практике широко применяется при депонировании вкладов населения, формировании фонда возмещения (амортизационного фонда) если известны ежегодные отчисления.
Фактор показывает, какая сумма будет накоплена на счете при заданной ставке, если регулярно в течение определенного периода откладывать на счет 1 денежную единицу.
Формирование фонда возмещения. Эта функция используется для определения равномерных периодических платежей, которые необходимо осуществлять в течение заданного периода, чтобы к концу срока иметь на счёте, приносящем доход по заданной ставке, определенную сумму денег:
 . (5)
. (5)
Фактор показывает, сколько нужно откладывать на счёт регулярно в течение определённого времени, чтобы при заданной ставке дохода иметь на счёте к концу этого срока одну денежную единицу.
Взнос на амортизацию – эта функция используется для определения аннуитетных платежей в счёт погашения кредита, выданного на определенный период при заданной ставке:
 . (6)
. (6)
Фактор показывает, какими должны быть аннуитетные платежи в счет погашения кредита в одну денежную единицу, выданного под определённый процент на определённый период.
Задачи
Решите две задачи в соответствии с вариантом.
Номера задач выбираются по табл. 1 в по последним двум цифрам номера зачётной книжки.
Например, номер зачётной книжки – 57849. В этом случае первая задача – № 18, а вторая задача – № 7.
Таблица 1
Варианты к заданию 3
| Последняя цифра шифра | ||||||||||
| Номер первой задачи | ||||||||||
| Предпоследняя цифра шифра | ||||||||||
| Номер второй задачи |
Условия задач к третьему заданию:
1. Рассчитайте будущую стоимость вложенных 100 денежных единиц при начислении процентов в течение 5 периодов для простого и сложного процента при ставке 10 %.
2. Какая сумма будет накоплена на счёте к концу второго года, если сегодня положить $1000 на счёт, приносящий 14% годовых. Каково начисление процентов в конце каждого года, квартала, месяца?
3. Определите текущую стоимость $1000, которые будут получены в конце года при 10 % ставке. Каково начисление процентов в конце каждого года, квартала, месяца?
4. Договор аренды квартиры составлен на один год. Определите текущую стоимость арендных платежей при 11% ставке дисконтирования, если арендная плата в размере $6000 выплачивается в конце года; и если арендная плата в размере $500 выплачивается в конце каждого месяца.
5. Оцените текущую стоимость права получения чистого рентного дохода в 100 денежных единиц на протяжении 4 лет при ставке 10%.
6. Вкладчик депонирует $1 в конце каждого года в течение 4 лет при ставке 10%. Определите сумму средств на счёте.
7. Определите сумму, которая будет накоплена на счёте, приносящем 12 % годовых, к концу 6-го месяца, если ежемесячно откладывать на счет $ 1000.
8. Вкладчику необходимо через 4 года иметь на счёте $1. Определите размер платежей при ставке 20%.
9. Определите, какими должны быть платежи, чтобы к концу 8 года иметь $10000 на счёте, приносящем 14% годовых. Каково поступление платежей в конце каждого года, квартала, месяца?
10. Сумма заёмных средств 331,2 р. Какие суммы необходимо выплачивать, чтоб рассчитаться по данному займу через 4 года. Процент платы за кредит составляет 8 %.
11. На покупку недвижимости выдан кредит в размере $10000 на 5 лет под 15% годовых. Определить размер платежей. Каково начисление процентов в конце каждого года, квартала, месяца?
12. На покупку недвижимости выдан кредит в размере $10000 на 5 лет под 15% годовых, погашение ежегодное. Рассчитать остаток долга по кредиту на конец 3-го года.
13. Производственный корпус был куплен за 6500 тыс. руб. с отсрочкой платежа на 3 года. Определить текущую стоимость корпуса, если бы расчет был произведен сразу, из расчета 15 % годовой ставки.
14. При сдаче в аренду офисного центра генерируется следующий поток доходов: 1-й год 6500 тыс. р.,2-й год 7000 тыс. р., 3-й год 8000 тыс. р., 4-й год 9500 тыс. р. Определить текущую стоимость потока доходов, при ставке 13 % годовых.
15. Семья располагает суммой 150 тыс. р. Определите покупательскую способность этой суммы через 3 года, при темпах инфляции 10, 14 и 18%.
16. Через сколько лет 500 тыс. руб. будут иметь покупательскую способность 212 тыс. руб. при темпах инфляции 10% в год.
17. Инвестор имеет возможность разместить свой капитал в $100000 в двух проектах на 5 лет. Первый проект предполагает вложение средств в строительство офиса с удвоением капитала за указанное время. Второй – строительство магазина и 13% годового дохода. Дайте рекомендацию инвестору, какой проект следует предпочесть. Задачу решить двумя способами.
18. Для покупки дома необходима сумма 675 тыс. р. Ежемесячно семья может откладывать 3 тыс. руб. под 9% годовых с ежемесячным начислением процентов. Определить через какое время будет накоплена необходимая сумма.
19. В рекламе утверждается, что, вложив сегодня в строительство гостиницы 13 420 руб., вы будете получать ежегодно по 2000 руб. в течение 10 лет. Проанализируйте данный вариант вложения средств при темпах инфляции 10%. Определите какой инфляционный процент отслеживается.
20. На протяжении 20 лет ежегодный доход от сдачи в аренду складского комплекса составляет 650 тыс. руб. По окончании этого срока объект продается за 3 770 тыс. руб. Определите текущую стоимость денежных потоков при 11% ставке дисконта.