I этап. Запись задачи в симплекс-таблицу.

Между системой ограничений задачи и симплекс-таблицей взаимно однозначное соответствие:

· Строчек в таблице столько, сколько равенств в системе ограничений (+2); а столбцов столько, сколько переменных (+2).

· Базисные переменные заполняют первый столбец, свободные и базисные – верхнюю строку таблицы.

· Каждая строка таблицы соответствует уравнению.

· Коэффициенты целевой функции записываются с противоположными знаками.

· В правом нижнем углу первоначально записывается 0, если в функции нет свободного члена.( На этом месте (в правом нижнем углу) будет значение целевой функции, которое при переходе от одной таблице к другой должно увеличиваться). Итак, нашей системе ограничений соответствует табл. 1 и можно переходить ко II этапу решения.

Таблица 1

свобод. базис		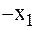	-х3	-х4	-х5	правые части
							50/1=50
							-
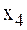
							80/2=40 min
F	–5	–3

II этап. Проверка опорного плана на оптимальность.

Данной таблице соответствует опорный план: 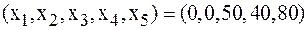. Свободные переменные равны 0, а базисные переменные принимают значения чисел столбца свободных членов. Значение целевой функции

Наша задача проверить, является ли данный опорный план оптимальным, для этого необходимо просмотреть индексную строку – строку целевой функции F.

Возможны ситуации:

1) в индексной F–строке нет отрицательных элементов. Значит, план оптимален, можно выписать решение задачи. Целевая функция достигла своего оптимального значения, равного числу, стоящему в правом нижнем углу. Переходим к IV этапу;

2) в индексной строке есть хотя бы один отрицательный элемент, в столбце которого нет положительных. Тогда делаем вывод о том, что целевая функция неограниченно возрастает;

3) в индексной строке есть отрицательный элемент, в столбце которого есть хотя бы один положительный. Тогда переходим к III этапу, улучшаем опорный план, пересчитывая таблицу.

III этап. Улучшение опорного плана.

1. Из отрицательныхэлементов индексной F–строки выберем наибольший по модулю, назовем соответствующий ему столбец разрешающим и пометим .

2. Чтобы выбрать разрешающую строку, необходимо вычислить отношения элементов столбца свободных членов к только положительным элементам разрешающего столбца. Выбрать из полученных отношений минимальное. Соответствующий элемент, на котором достигается минимум, называется разрешающим. Будем выделять его квадратом.

В нашем примере, элемент – разрешающий. Строка, соответствующая этому элементу, тоже называется разрешающей.

Таблица 2

свобод. базис		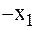	-х3	-х4	-х5	правые части
							50/1=50
							-
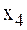
							80/2=40 min
-F	–5	–3

3. Выбрав разрешающий элемент, делаем перечет таблицы по следующим правилам.

3.1. В новой таблице, таких же размеров, что и ранее, переменные при разрешающем элементе меняем местами, что соответствует смене базисов. В нашем примере: входит в базис, вместо , которая выходит из базиса, и теперь свободная (меняются местами элементы столбцов Х₁ и Х₅).

3.2. На месте разрешающего элемента (который теперь в столбце Х₅)записываем обратное ему число

3.3. Элементы разрешающей строки делятся на разрешающий элемент.

3.4. Элементы разрешающего столбца делятся на разрешающий элемент и записываются с противоположным знаком

Таблица 3

свобод. базис	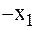-х3	-х4	-х5	правые части


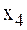
X₁
-F

3.5. Все остальные элементы табл. 2.6 пересчитываем по правилу прямоугольника (в любом порядке).

Правило прямоугольника:

Пусть мы хотим посчитать элемент, например Соединяем пересчитываемый элемент мысленно с разрешающим, находим произведение .

Вычитаем произведение элементов, находящихся на другой диагонали получившегося прямоугольника. Разность делим на разрешающий элемент.

Итак, . Записываем 10 на место, где было 50.

Аналогично:

, , , .

Имеем в новом базисе пересчитанную табл. 2.8.

Таблица 4

свобод. базис	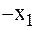-х3	-х4	-х5	правые части

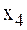
					40/1=40
X₁					40*2/1=80
-F

Базисными переменными теперь являются переменные . Значение целевой функции стало равно 200, т.е. увеличилось. Чтобы проверить данное базисное решение на оптимальность, надо перейти опять ко II этапу.

Для этого проверим индексную строку и, увидев в ней отрицательный элемент , назовем ему соответствующий столбец – разрешающим. Составим соотношения правых частей к только положительным элементам разрешающего столбца, выберем среди них минимальное: . Определим разрешающий элемент 1, теперь пересчет осуществляем согласно правилам 3.1–3.5.

свобод. базис	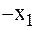-х3	-х4	-х5	правые части



-F

После пересчета таблицы убеждаемся, что в индексной строке последней таблицы нет отрицательных элементов, следовательно, задача решена, базисный план оптимален.