Алгоритм графического метода решения ЗЛП.
В системе координат построить прямые по уравнениям, соответствующим каждому неравенству системы ограничений;
найти полуплоскость решения каждого неравенства системы (обозначить стрелками). Для определения полуплоскости необходимо выбрать любую контрольную точку, не лежащую на данной прямой. Подставить ее координаты в систему ограничений. Если неравенство выполняется, то нужно выбрать полуплоскость, содержащую контрольную точку. Если неравенство не выполняется нужно выбрать полуплоскость, не содержащую контрольную точку. В качестве контрольной точки рекомендуется выбирать точку с координатами (0;0);
найти многоугольник (многоугольную область) решений системы ограничений как пересечение полуплоскостей;
построить вектор нормали N. Начало вектора нормали в точке с координатами (0;0), конец вектора в точке с координатами (с1, с2);
через начало координат построить линию уровня, перпендикулярно к вектору нормали;
перемещать линию уровня параллельно самой себе по области решения в угловые точки, достигая max f при движении вектора N и достигая точки «выхода» (min f при движении достигая точки «входа»);
найти координаты точки max (min). Для этого необходимо решить систему уравнений прямых, которые пересекаются в этой точке или определить координаты по графику;
вычислить значение целевой функции в этой точке (ответ).
Задача. Решить графическим методом следующую задачу линейного программирования:
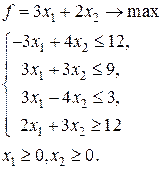
.
1. Найдем общую часть всех полуплоскостей решений. Получим, что область допустимых решений представляет собой четырехугольник 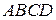
2. Построим вектор-градиент 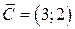 .
.
3. Построим прямую 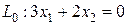 , проходящую через начало координат перпендикулярно
, проходящую через начало координат перпендикулярно 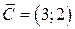 .
.
4. Перемещаем прямую  параллельно и пересечем ОДР. Последнее пересечение с ОДР будет в точке
параллельно и пересечем ОДР. Последнее пересечение с ОДР будет в точке 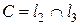 , которая соответствует максимуму целевой функции.
, которая соответствует максимуму целевой функции.
5.Определим координаты точки 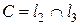 , решая систему
, решая систему 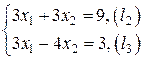 .
.
Подставив координаты точки 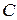 в целевую функцию, получим
в целевую функцию, получим
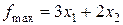 :
:
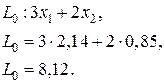
Точка С (2,14; 0,85) является точкой максимума 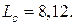
Ответ: Fmax= 8,12 при x (2,14; 0,85)