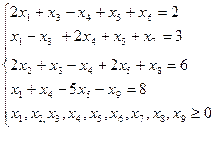Переход от канонической к стандартной.

Систему уравнений (ограничений) преобразовываем в эквивалентную ей систему неравенств, а целевую функцию записать через переменные полученной системы неравенств.

1. Приводим к единичному базису методом гауса. Приравняем все свободные переменные к 0, т.е. x_m+1=x_m+2=0 то получим первоначальное базисное решение.

2. Выражаем все базисные переменные через свободные.

Х₁=b₁-a₁,_m+1x_m+1-..-a1,nxn>=0

Xm=bm-am,m+1-…-amnxn>=0

3. В функция цели вместо базисных переменных подставить их через переменные.

Пример. 1.

Записать в форме основной ЗЛП следующую задачу

Найти максимум функции F= при условиях

ответ