Занятие №1. Расчет элементов прямоугольного профиля на прочность по нормальным сечениям с одиночной арматурой

Цель расчета –определить минимальный расход продольной арматуры каркасов (для балок) или арматуры сеток в нижней растянутой зоне сечения элементов.

Контрольные вопросы для самопроверки знаний:

1. Какие элементы относятся к классу изгибаемых?

а) Изгибаемыми называются элементы, в которых в поперечном сечении при действии внешних нагрузок возникает изгибающий момент в середине их пролета.

б) Изгибаемыми называются элементы, в которых в поперечных сечениях при действии внешних нагрузок возникают изгибающие моменты и поперечные силы.

в) Изгибаемыми называются элементы, в которых возникают изгибающие моменты при действии равномерно распределенных нагрузок и сосредоточенных сил.

2. Расчетная схема усилий в нормальном сечении изгибаемого элемента с одиночной арматурой?

3. Какие характеристики бетона и арматуры учитываются при расчете изгибаемых элементов с одиночной арматурой на прочность по нормальным сечениям?

4. Как назначается величина защитного слоя бетона для растянутой арматуры?

5. Установите критерий одиночного армирования изгибаемого элемента?

а) ξ< 0 ,

б) ξ < ξ _R,

в) h₀ < 180 мм.

5. Расчетная формула положения границы сжатой зоны в нормальном сечении изгибаемого элемента?

6. Условие прочности нормального сечения изгибаемого элемента с одиночной арматурой?

7. Из каких условий назначается класс бетона по прочности на сжатие для изгибаемого элемента с одиночной арматурой?

а) Из условия минимального продольного армирования;

б) Из условия обеспечения минимальной высоты изгибаемого элемента;

в) Из условий эксплуатации изгибаемого элемента по обеспечению требуемых марок по морозостойкости и водостойкости.

Изгибаемыми называются элементы, в которых в поперечном сечении при действии внешней нагрузки возникают изгибающие моменты и поперечные силы в зависимости от расчетной схемы приложения нагрузки и граничных условий закрепления элемента. На рис. 1 приведен пример расчетной схемы изгибаемого однопролетного элемента, загруженного равномерно распределенной нагрузкой с двумя возможными схемами разрушения по нормальному и наклонному сечениям.

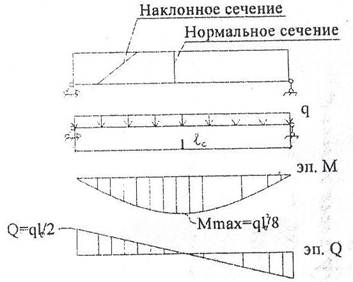
Рис. 1. Расчетная схема изгибаемого элемента

Расчетная схема внутренних усилий и эпюра напряжений в прямоугольном поперечном сечении изгибаемого железобетонного элемента с одиночной арматурой приведена на рис. 2.

Рис. 2. Схема внутренних усилий и эпюра напряжений в поперечном

сечении изгибаемого железобетонного элемента с одиночной арматурой

Ниже приведены основные расчетные формулы и порядок расчета прочности нормального сечения железобетонного элемента с одиночной арматурой.

Условие прочности нормального сечения изгибаемого железобетонного элемента записывается в виде:

M < R_s* A_s (h₀ – 0.5*x) , ( 1 )

где: R_s – расчетное сопротивление арматуры на растяжение, принимаемое согласно табл. 31 / Н/см^2/ / 1 /;

А_s – минимальный расход продольной растянутой арматуры в / см² /;

h₀- рабочая высота сечения изгибаемого элемента в / см /:

h₀ = h – a_s , ( 2 )

где: h – высота сечения элемента (балки, плиты) в / см /;

a_s – расстояние от нижней растянутой зоны сечения элемента до центра тяжести растянутой арматуры в / см /:

- при расположении арматуры в один ряд: a_s = a + 0.5*d_s , где d_s – диаметр искомой арматуры и «а» - защитный слой бетона: не менее 30 мм и не менее диаметра арматуры «d_s»;

- при расположении арматуры вплотную в два ряда (без зазора):

a_s = a + d_s;

х – абсолютная высота сжатой зоны сечения изгибаемого элемента:

х = R_s*A_s/ R_b*b , ( 3 )

где: R_b – расчетное сопротивление бетона изгибаемого элемента на сжатие согласно табл. 23 в МПа или Н/см² в зависимости от размерности R_s / 2 /.

Последовательность практического расчета прочности нормального сечения изгибаемого элемента с одиночной арматурой.

Дано: М, b, h, R_s, R_b.

Необходимо определить минимальный расход продольной растянутой арматуры в изгибаемом элементе (балке или в плите).

1. Определяется значение рабочей высоты сечения элемента с учетом защитного слоя бетона:

h₀= h – a_s ; ( 4 )

2. Определяется минимальный расход продольной растянутой арматуры:

); ( 5 )

3. Конструирование изгибаемого элемента (балки или плиты) возможно в дальнейшем по двум направлениям:

а) задаваясь количеством стержней по сортаменту определяют диаметр арматуры;

б) задаваясь диаметром арматуры по сортаменту определяют количество стержней арматуры.

Таким образом устанавливают фактический расход арматуры A_s^*, который должен быть не менее расчетного значения A_s.

4. Определяются абсолютное и относительное значения сжатой зоны сечения элемента:

х = R_s*A_s^*/ R_b* b , ξ = х/h₀. ( 6 )

5. Определяется граничное значение относительной высоты сжатой зоны бетона сечения элемента :

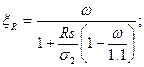( 7 )

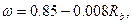(для тяжелых бетонов);

6. Выполнить сравнение: ξ < = ξ _R : ( 8 )

а) если условие ( 8 ) выполняется определить несущую способность элемента М^*, которая должна быть больше изгибающего момента от действия внешней нагрузки М:

M* = R_s* A_s^* ( h₀ – 0.5*x ); ( 9 )

Условие прочности выполняется.

б) если условие ( 8 ) не выполняется, то необходимо изменить исходные данные по назначению класса бетона по прочности на сжатие и (или) увеличить высоту сечения элемента (балки или плиты) и повторить расчеты до выполнения условия ( 8 ).

Пример расчета №1.Определить минимальный расход продольной растянутой арматуры изгибаемого элемента при следующих исходных данных:

Дано: Балка прямоугольного сечения с размерами 25х50 см (bxh) запроектирована из тяжелого бетона класса В25, R_b = 13 МПа. Продольная арматура класса А400, R_s = 350 МПа. Величина изгибающего момента М = 245 кН*м. Вычертить эскиз армирования балки.

1. Определяем рабочую высоту сечения балки при условии, что арматура располагается в один ряд и максимально доступный диаметр арматуры 30мм:

h₀ = 50 – 3 – 1.5 = 45.5 см.

2. Определяем минимальный расход растянутой арматуры:

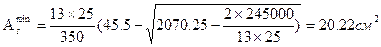
3. Согласно сортамента арматуры принимаем армирование балки :

A_s^* = 12.32 + 9.82 = 22.14 см² ( 2Ø28 + 2Ø25 ) с процентом армирования: 2214/25х45.5 = 1.95 %, что меньше 3%.

4. Определяем параметры сжатой зоны сечения балки:

х = 350х22.14/13х25 = 23.84 см; ξ = 23.84/45.5 = 0.524.

5. Граничное значение относительной высоты сжатой :

; ;

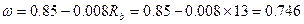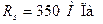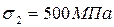
Условие ( 8 ) выполняется.

6. Несущая способность балки:

М* = 350х22.14( 45.5 – 11.92 ) = 260.2 кН*м, что больше М = 245 кН*м. Условие прочности выполняется.

Таблица 1

Варианты заданий

№№	В, мм	h, мм	Класс бетона	Класс арматуры	Изг.момент кН*м
			В25	А300	212.5
			В30	А400	230.7
			В20	А300	125.6
			В25	А400	235.9
			В20	А300	118.3
			В20	А400	54.2
			В25	А300	126.6
			В25	А400	263.7
			В30	А300	232.5
			В30	А300	265.7
			В25	А300	308.5
			В30	А400	178.2
			В25	А300	301.5
			В30	А400	199.5
			В20	А300	61.5
			В25	А400	232.7
			В30	А300	108.6
			В25	А300	23.8
			В20	А400	21.5
			В30	А300	65.5
			В25	А400	301.3	А300	65.5
			В25	А400	301.3
			В25	А300	29.9
			В20	А400	34.3
			В30	А300	145.8
			В30	А400	350.6
			В25	А300	232.3
			В30	А300	31.4
			В25	А400	280.1
			В25	А300	60.4
			В25	А400	105.3