Формула полной вероятности и формула Байеса

Пусть событие А может произойти только совместно с одним из событий Н₁, Н₂,…, Н_п, , называемых гипотезами и образующими полную группу несовместных событий (p(H1) +p(H2) +…+ p(Hn) = 1).

Вероятность события А, наступающего совместно с гипотезами Н₁, Н₂,…, Н_п, равна (формула полной вероятности):

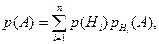(9.1)

где p(H_i) – вероятность i- й гипотезы, а 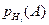– вероятность события А при условии реализации этой гипотезы.

 

Доказательство. Можно считать событие А суммой попарно несовместных событий АН₁, АН₂,…, АН_п. Тогда из теорем сложения и умножения следует, что

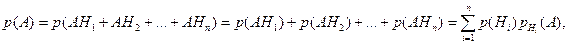
что и требовалось доказать.

 

Пример. Имеются три одинаковые урны с шарами. В первой из них 3 белых и 4 черных шара, во второй – 2 белых и 5 черных, в третьей – 10 черных шаров. Из случайно выбран-ной урны наудачу вынут шар. Найти вероятность того, что он белый.

Решение. Будем считать гипотезами Н₁, Н₂ и Н₃ выбор урны с соответствующим номером. Так как по условию задачи все гипотезы равновозможны, то

Найдем условную вероятность А при реализации каждой гипотезы:

Тогда

Пусть в результате испытания произошло событие А, которое могло наступить только

вместе с одним из событий H1, H2,…Hn,образующих полную группу событий .

Требуется найти вероятность события H_i после испытания, когда событие Аимело место, т.е. p_A (H_i), i = 1,2,…n.Для нахождения этих вероятностей используют формулу Байеса (формулу вероятности гипотез):

(9.2)

 

Действительно, откуда следует справедливость формулы Байеса.

 

Замечания.

1) Вероятности PA(H₁)называются послеопытными (апостериорными) вероятностями гипотез H_i,а вероятности P(H_i)- доопытными (априорными) вероятностями гипотез Hi.Эти вероятности различаются.

2) Знаменатель в правой части формулы Байеса совпадает с правой частью формулы полной вероятностии равен P(A).

 

Пример. После двух выстрелов двух стрелков, вероятности попаданий которых равны 0,6 и 0,7, в мишени оказалась одна пробоина. Найти вероятность того, что попал первый стрелок.

Решение. Пусть событие А – одно попадание при двух выстрелах, а гипотезы: Н₁ – первый попал, а второй промахнулся, Н₂ – первый промахнулся, а второй попал, Н₃ – оба попали, Н₄ – оба промахнулись. Вероятности гипотез: р(Н₁) = 0,6·0,3 = 0,18, р(Н₂) = 0,4·0,7 = 0,28, р(Н₃) = 0,6·0,7 = 0,42, р(Н₄) = 0,4·0,3 = 0,12.Тогда PA(H₁) = PA(H₂)= 1, PA(H₃)= PA(H₄)= 0. Следовательно, полная вероятность р(А) = 0,18·1 + 0,28·1 + 0,42·0 + 0,12·0 = 0,46. Применяя формулу Байеса, получим: