Вероятность произведения событий

Вероятность события А,вычисляемая при условии, что событие Впроизошло, называется условной вероятностью события и обозначается p_B(A).

Событие В называется независимымот события А, если появление события А не изменяет вероятности В, то есть p_A (B)= р (В).

Примеры:

1) пусть событие А – извлечение из колоды в 32 карты туза, а событие В – то, что и вторая вынутая из колоды карта окажется тузом. Тогда, если после первого раза карта была возвращена в колоду, то вероятность вынуть вторично туз не меняется: Если же первая карта в колоду не возвращается, то осуществление события А приводит к тому, что в колоде осталась 31 карта, из которых только 3 туза. Поэтому

2) если событие А – попадание в самолет противника при первом выстреле из орудия, а В – при втором, то первое попадание уменьшает маневренность самолета, поэтому p_B(A) увеличится по сравнению с р(А).

Теорема (теорема умножения). Вероятность произведения двух событий равна произведению вероятности одного из них на условную вероятность другого при условии, что первое событие произошло:

р(АВ) = р(А)·p_A(B) = р(В)·p_B(A) (8.1)

Доказательство. Воспользуемся обозначениями теоремы сложения (п.7). Тогда для вычисления р_А(В) множеством возможных исходов нужно считать т_А(так как А произошло), а множеством благоприятных исходов – те, при которых произошли и А и В - т_АВ. Следовательно,

откуда следует утверждение теоремы.

Пример. Для поражения цели необходимо попасть в нее дважды. Вероятность первого попадания равна 0,2, затем она не меняется при промахах, но после первого попадания увеличивается вдвое. Найти вероятность того, что цель будет поражена первыми двумя выстрелами.

Решение. Пусть событие А – попадание при первом выстреле, а событие В – попадание при втором. Тогда р (А) = 0,2, p_B(A) = 0,4, р (АВ) = 0,2·0,4 = 0,08.

Следствие 1. Вероятность произведения двух независимых событий равна произведению вероятностей этих событий, т. е.:

P(AB) = P(A)P(B). (8.2)

Следствие 2. Вероятность появления хотя бы одного из событий А1,A2…An.,независимых в совокупности, равна разности единицы и произведения вероятностей противоположных событий :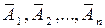

(8.3)

При решении задач теоремы сложения и умножения обычно применяются вместе.

Пример. Два стрелка делают по одному выстрелу по мишени. Вероятности их попадания при одном выстреле равны соответственно 0,6 и 0,7. Найти вероятности следующих событий:

А – хотя бы одно попадание при двух выстрелах;

В – ровно одно попадание при двух выстрелах;

С – два попадания;

D – ни одного попадания.

Решение. Пусть событие Н₁ – попадание первого стрелка, Н₂ – попадание второго. Тогда

А = Н₁ + Н₂, В =Н₁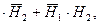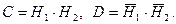События Н₁ и Н₂ совместны и независимы, поэтому теорема сложения применяется в общем виде, а теорема умножения – в виде (2.8). Следовательно, р(С) = 0,6·0,7 = 0,42, р(А) = 0,6 + 0,7 – 0,42 = 0,88,

р(B) = 0,6·0,3 + 0,7·0,4 = 0,46 (так как события и 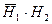несовместны),

р(D) = 0,4·0,3 = 0,12. Заметим, что события А и D являются противоположными, поэтому

р(А) = 1 – р(D).

Пример. Сколько нужно произвести бросков монеты, чтобы с вероятностью не менее 0,9 выпал хотя бы один герб?

Решение. Вероятность выпадения герба при одном броске равна вероятности противопо-ложного события (выпадения цифры) и равна 0,5. Тогда вероятность выпадения хотя бы одного герба при п выстрелах равна 1- (0,5)^п . Тогда из решения неравенства 1- (0,5)^п > 0,9

следует, что п > log₂10 ≥ 4.