Элементы комбинаторики.

Комбинаторика – наука, изучающая комбинации, которые можно составить по определенным правилам из элементов некоторого конечного множества.

 

Пусть задано множество, содержащее конечное число (n) элементов. Такие множества будем называть конечными, и обозначать {a,b,c,d, . . .s}.

 

Перестановки– это комбинации, составленные из всех п элементов данного множества и отличающиеся только порядком их расположения. Число всех возможных перестановок:

(5.1)

 

Если n=3: (a,b,c), (a,c,b), (b,a,c), (b,c,a), (c,a,b), (c,b,a). Р₃= 3!=6.

Пример. Сколько различных списков (отличающихся порядком фамилий) можно составить из 7 различных фамилий?

Решение. Р₇ = 7! = 2·3·4·5·6·7 = 5040.

 

Размещения – упорядоченные комбинации из т элементов данного множества (то есть, отличающиеся либо составом элементов, либо их порядком). Число всех возможных размещений:

(5.2)

Если n=3, m=2: (a,b), (a,c), (b,a), (b,c), (c,a), (c,b).

Пример. Сколько возможно различных вариантов пьедестала почета (первое, второе, третье места), если в соревнованиях принимают участие 10 человек?

Решение.

 

Сочетания – неупорядоченные наборы из т элементов множества (то есть наборы, отличающиеся только составом элементов, их порядок не имеет значения). Число всех возможных сочетаний:

(5.3)

 

Если n=3, m=2: (a,b), (a,c), (b,c),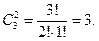

Пример. В отборочных соревнованиях принимают участие 10 человек, из которых в финал выходят трое. Сколько может быть различных троек финалистов?

Решение. В отличие от предыдущего примера, здесь не важен порядок финалистов, следовательно, ищем число сочетаний из 10 по 3:

(5.4)

 

Размещение с повторениями по k элементов может содержать любой элемент сколько угодно раз от 1 до k включительно, или не содержать его совсем, т.е. каждое размещение с повторениями из n элементов по k элементов может состоять не только из различных элементов, но из k каких угодно и как угодно повторяющих элементов. Число размещений с повторениями вычисляется по формуле:

(5.5)

Пример. Сколько четырехзначных цифр можно составить из 9 цифр (исключая число 0)?

 

Сочетание с повторениями из n элементов по k элементов может содержать любой элемент сколько угодно раз от 1 до k включительно, или не содержать его совсем, т.е. каждое сочетание с повторениями из n элементов по k элементов может состоять не только из k различных элементов, но из k каких угодно и как угодно повторяющих элементов.

Следует отметить, что если, например два сочетания по k элементов отличаются друг от друга только порядком расположения элементов, то они не считаются различными

сочетаниями.

Число размещений с повторениями вычисляется по формуле:

(5.6)

Пример. Каждый шарик раскрашивают тремя красками. Сколько шариков с различным сочетанием цветов можно получить, если используется семь красок?