Комптон эффектісі
Американ ғалымы Комптон жарықтың жеңіл заттардан шағылғанда, шағылған жарықтың толқын ұзындығы артатынын байқады. Комптон бұл құбылысты түсіндіру үшін импульс пен энергияның сақталу заңын пайдаланды.
Комптон эффектісін сипаттайтын формула:
 немесе
немесе  .
.
Электрон үшін Комптонның толқын ұзындығы:

Кванттық механика негіздері
Микробөлшектердің қозғалыс заңдылықтарын зерттейтін физиканың бөлімін кванттық механика деп атайды.
Элементар бөлшектерді және осы бөлшектердің аз санынан тұратын денелерді микробөлшектер деп атаймыз. Француз ғалымы де Бройль жарықтың екі жақтылық қасиеті электронға да орындалады деген болжам ұсынды, яғни электронның механикалық қозғалысына толқындық қасиет сәйкес келеді және бұл толқынның ұзындығы келесі формуламен анықталады:
 немесе
немесе  ,
,
мұндағы: р - дене импульсы,  -Планк тұрақтысы.
-Планк тұрақтысы.
Бұл өрнек де Бройль формуласы деп аталады.
Ал бөлшектің кинетикалық энергиясы  екенін ескерсек, онда де Бройльдің толқын ұзындығы кинетикалық энергия арқылы келесі түрде өрнектеледі:
екенін ескерсек, онда де Бройльдің толқын ұзындығы кинетикалық энергия арқылы келесі түрде өрнектеледі:
 .
.
Потенциалдар айырмасы  -ға тең үдетуші электр өрісінен өткен электронның энергиясы:
-ға тең үдетуші электр өрісінен өткен электронның энергиясы:

Соңғы өрнекті ескере отырып де Бройль формуласын келесі түрде өрнектеуге болады:
 ,
,
мұндағы:  .
.
 .
.
Американ ғалымы Томсон жұқа металл фольгалардан шапшаң электрондарды өткізгенде экранда дифракциялық көрініс бақылады.

Бұл дифракциялық көрініс Брэгг-Вульф шартымен сипатталады:
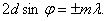
Кванттық механикада кез-келген микробөлшектің қозғалысына толқындық қозғалыс сәйкес келеді және бұл толқындық қозғалыс сол бөлшектің де Бройльдық толқын ұзындығымен сипатталады.
де Бройль толқынының амплитудасының квадраты микробөлшектің кеңістіктің берілген нүктесінде болу ықтималдығын анықтайды. Микробөлшектің кеңістіктің берілген нүктеде болу ықтималдығын анықтау үшін кеңістік пен уақыттың функциясы толқындық функция енгізілген.
 функциясы толқындық функция немесе пси функция деп аталады.
функциясы толқындық функция немесе пси функция деп аталады.
Пси функциясының модулінің квадраты микробөлшектің кеңістіктің берілген нүктесінде болу ықтималдығын анықтайды.
Толқындық функция келесі шартты қанағаттандыруы қажет:
 .
.
Бұл шарт нормалану шарты деп аталады.
Өзара байланысқан шамаларды анықтаудағы қателіктердің көбейтіндісі Планк тұрақтысынан кіші болмайды.
Кез-келген А және В байланысқан шамалары үшінГейзенбергтің анықталмаушылық принципі келесі түрде жазылады:
 .
.
Координата мен импульс үшінГейзенбергтің анықталмаушылық принципі.
Координата мен импульсті анықтаудағы қателіктердің көбейтіндісі Планк тұрақтысынан кіші болмайды, яғни

Энергия мен уақыт үшін Гейзенбергтің анықталмаушылық принципі:
 ,
,
мұндағы:  -Планк тұрақтысы.
-Планк тұрақтысы.
Шредингер теңдеуі
Релятивистік емес кванттық механиканың негізгі теңдеуін неміс ғалымы Шредингер алды. Сондықтан бұл теңдеу  Шредингер теңдеуі деп аталады.
Шредингер теңдеуі деп аталады.

мұндағы:  ,
, 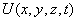 - күштік өрістегі бөлшектің потенциалдық энергиясы.
- күштік өрістегі бөлшектің потенциалдық энергиясы.
 - функциясына қойылатын шарттар:
- функциясына қойылатын шарттар:
1.  - функциясы шекті, үздіксіз, бір мәнді болу қажет;
- функциясы шекті, үздіксіз, бір мәнді болу қажет;
2.  - функциясы уақыт пен координаттар бойынша дифференциалы үздіксіз болуы қажет;
- функциясы уақыт пен координаттар бойынша дифференциалы үздіксіз болуы қажет;
3.  - функциясының модулінің квадратының интегралы болу керек және бұл интеграл шекті болу керек.
- функциясының модулінің квадратының интегралы болу керек және бұл интеграл шекті болу керек.
Микроәлемде өтетін көптеген физикалық құбылыстарды қарастырғанда, мысалы атомдағы электронның күйін зерттегенде уақытқа тәуелсіз Шредингер теңдеуін қарастыру қажет болады. Ол үшін Шредингер жалпы теңдеуінен уақытты қысқарта отырып, Шредингердің стационар теңдеуі алынады.
Шредингер теңдеуіндегі пси функциясының шешімін келесі түрде іздейік: 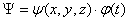 ,
,
мұндағы:  айнымалысы координаталардың,
айнымалысы координаталардың,  - уақыттың функциясы болып табылады. Айнымалыларды бөле отырып Шредингердің стационар теңдеуі алынады
- уақыттың функциясы болып табылады. Айнымалыларды бөле отырып Шредингердің стационар теңдеуі алынады
 .
.
Шредингер теңдеуін қанағаттандыратын  функциясын осы теңдеудің меншікті функциясы деп атайды, ал осы теңдеуді қанағаттандыратын толық энергияның мәнін меншікті мән деп атайды.
функциясын осы теңдеудің меншікті функциясы деп атайды, ал осы теңдеуді қанағаттандыратын толық энергияның мәнін меншікті мән деп атайды.
Еркін электрон қозғалысы
Бөлшектің еркін қозғалысы кезінде оның толық энергиясы кинетикалық энергиясына тең болады. Бұл жағдай үшін Шредингер теңдеуі келесі түрде жазылады:
 .
.
Бұл теңдеудің шешімі

мұндағы: А, В- тұрақты шамалар.
Еркін электронның қозғалысына монохроматты жазық де Бройль толқыны сәйкес келеді.
Потенциал “шұңқырдағы” электрон
Бір өлшемді шексіз терең потенциалды шұңқырдағы электронның қозғалысын қарастырайық.

| Электронның шұңқыр ішіндегі және тыс жердегі потенциалдық энергиясы келесі мәндерді қабылдайды
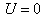 ( (  ), ),
 ( ( 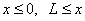 ).
Потенциалды өрісте қозғалатын электронның қозғалысы үшін Шредингер теңдеуін қолдана отырып, алатынымыз ).
Потенциалды өрісте қозғалатын электронның қозғалысы үшін Шредингер теңдеуін қолдана отырып, алатынымыз
|

Электронның потенциалды шұңқырдан тыс жерде табылу ықтималдылығы нольге тең. Сол себепті терең потенциалды шұңқырдағы электронның қозғалысын зерттейтін есеп төменде көрсетілген шекті шарттары бар келесі дифферециалдық теңдеуді шешуге келеді
 ,
,
мұндағы:  толқындық функция үшін шекті шарттар.
толқындық функция үшін шекті шарттар.
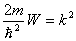 белгілей отырып, теңдеудің шешімін келесі түрде жазамыз:
белгілей отырып, теңдеудің шешімін келесі түрде жазамыз:

 шартынан
шартынан  және
және  екені алынады.
екені алынады.
 шартынан
шартынан  және
және  (
(  ) екені алынады.
) екені алынады.
Жоғарыдағы теңдеулерден  -ні қысқарта отырып электронның энергиясының меншікті мәнін табамыз
-ні қысқарта отырып электронның энергиясының меншікті мәнін табамыз
 ,
,
мұндағы: 
Потенциалдық шұңқырдағы электронның толық энергиясы тек дискретті мәндерді қабылдайды. Кванттық механикада дискреттік мәндерді қабылдайтын шамаларды квантталатын шамалар деп атайды.
Сондай-ақ потенциалды шұңқырдағы электронның меншікті функциясы келесі түрде жазылады:
 .
.