Инерция моменттерi

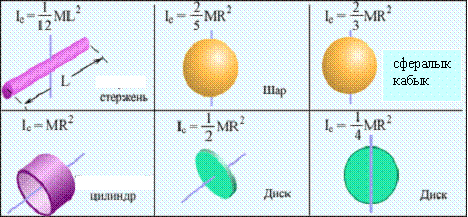
1. Жұқа дискiнiң: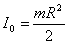

2. Стерженнiң: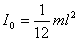

3. Цилиндрдiң:

4. Шардың: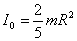

5. Материялық нүктенiң айналу осiне қатысты инерция моментi:

Дененiң кез-келген оське қатысты инерция моментi Штейнер теоремасы бойынша анықталады: ,

мұндағы:- ауырлық центрiмен айналу осі арасындағы ара қашықтық.

Айналмалы қозғалыстағы дененiң кинетикалық энергиясы:

Айналмалы қозғалыс кезiнде қатты дененiң кинетикалық энергиясы- оның инерция моментi мен бұрыштық жылдамдығының квадратының көбейтiндiсiнiң жартысына тең.

Жазық қозғалыстағы дененiң кинетикалық энергиясы- дененiң iлгерiлемелi және айналмалы қозғалыс кезiндегi кинетикалық энергияларының қосындысына тең болады.

Тұтас орта механикасы

Газдар мен сұйықтардың тепе-теңдiгiн және қозғалысын зерттегенде оларды үздiксiз тұтас орта түрiнде қарастырады.

Сұйықтардың тепе-теңдiгiн қарастыратын механиканың бөлiмiн – гидростатикадеп атайды.

Сұйықтар мен газдардың серпiмдi қасиетi мынадан байқалады: олардың жеке бөлiктерi бiр-бiрiне немесе олармен жанасатын денеге сұйық пен газдардың сығылу дәрежесiне тәуелдi болатын күшпен әсер етедi. Мұндай әсер қысыммен сипатталады.

Сөйтiп, сұйықтар мен газдарды сипаттайтын ең негiзгi шамалардың бiрi - қысым.

Қысым деп бетке түсетiн күштiң осы беттiң ауданына қатынасына тең шаманы айтады. Өлшем бірлігі .

Паскаль заңы.

Сұйық ішіне түсiрілген қысым барлық бағытқа бiрдей берiледi.

Сұйық iшiндегi қысым: .

Бұл қысымды кейде гидростатикалық қысым деп атайды.

Сұйықтардың қозғалысын зерттейтiн механиканың бөлiмiн – гидродинамикадеп атайды.

Сұйық бөлшектерiнiң қозғалысын зерттеудiң екі тәсiлi бар.

1.Лагранж тәсiлi

Бұл тәсiлде әрбiр жеке сұйық бөлшегiнiң кеңiстiктегi қозғалыс заңдылығы зерттеледi.

2.Эйлер тәсiлi

Бұл тәсiлде кеңiстiктiң белгiлi бiр нүктесiнен өтетiн сұйық бөлшектерiнiң жылдамдығы қарастырылады.

Сұйық бөлшектерiнiң қозғалысы - ағыс, ал сұйықтың қозғалысы- ағындеп аталады.

Кез келген нүктесiнде жүргiзiлген жанама сол нүктедегi сұйық бөлшегiнiң жылдамдықтарымен сәйкес келетiн сызықтарды ағын сызықтарыдеп атайды. Ағын сызықтарының жиiлiгi сол жерде сұйықтың жылдамдығын көрсетедi (сурет).

Мысалы суреттегi А нүктесiндегi сұйықтың жылдамдығы В нүктесiндегi сұйықтың жылдамдығынан үлкен болады. Ағын сызықтарымен шектелген сұйық бөлiгiн ағын сорғысыдеп атайды.

Кез келген нүктесiндегi сұйықтың жылдамдығының шамасы мен бағыты өзгермейтiн ағысты стационар ағысдеп атайды.

Ағыс сипатына байланысты екіге бөлiнедi.

Егер сұйық қабаттары бiр-бiрiмен араласпай, бiр-бiрiне параллель қозғалатын болса, мұндай ағыс – ламинар(қабатты) ағысдеп аталады.

Егер сұйық қабаттары бiр-бiрiмен араласып иiрiлiп қозғалатын болса, мұндай ағыс – турбуленттi (иiрiмдi)депаталады. Сығылмайтын тұтқыр емес сұйықты идеал сұйық деп, ал сығылатын тұтқыр сұйық реал сұйық деп аталады.

Ағынның үздiксiздiк теңдеуi

Суреттегiдей түрде жалғастырыл-ған екi ыдыс алайық. Жоғарғы ыдыстағы сұйық биiктiкке дейiн толтырылған делiк. Ендi екi ыдысты қосатын шүмегiн ашсақ, онда сұйықтың бiразы жоғарғы ыдыстан төменгi ыдысқа ағып өтедi. Айталық, уақыт iшiнде жоғарғы ыдыстағы сұйықтың деңгейi -ге төмендеп,

төменгi ыдыс толсын. Сұйық сығылмайды және үзiлмейдi деп есептесек, нда жоғарғы ыдыстан ағып кеткен сұйық көлемi мен төменгi ыдысқа құйылған сұйық көлемi тең болады:

мұндағы: - жоғарғы ыдыстың көлденең қимасы, - төменгi ыдыстың көлденең қимасы, бұл формуланың екi жағын -¹а бөлсек: немесе ,

мұндағы - жоғарғы ыдыстағы сұйық ағысының жылдамдығы, - төменгi ыдыстағы сұйық ағысының жылдамдығы. Сонда

Осы өрнектi ағынның үздiксiздiк теңдеуiдеп атайды. Ыдыстың көлденең қимасының сұйық ағысының жылдамдығына көбейтiндiсi тұрақты шама болады.

Сұйық ағысының жылдамдығы ыдыстың көлденең қимасына керi пропорционал.

Бернулли теңдеуi

Идеал сұйықтың қозғалысын (ағысын) сипаттайтын өрнектi 1738 жылы Д.Бернулли (1700-1782) тұжырымдады. Бернулли энергияның сақталу заңын пайдалана отырып, сұйық қысымының жылдамдыққа тәуелдiлiгiн анықтады. Бұл формуланы қорытып шығару үшiн көлденең қимасы әр түрлi түтiкшедегi идеал сұйықтың қозғалысын қарастырайық (сурет).

1 және 2 қималардың арасындағы сұйық массасының қозғалуын бақылайық. 1-ден кейiн, 2 қиманың алдында ағын болмаса да екi қима арасындағы сұйық массасы өз салмағы әсерiнен қозғала бастайды. Алайда, екi қима арасындағы сұйық өз массасымен ғана қозғалып қоймай, ол айырмасының әсерiнен де қозғалысқа келетiнiн айта кеткен жөн. Сонымен сыртқы күш жұмыс iстейдi. Мұндағы - 1 қимада iстелетiн жұмыс. - 2 қимада iстелетiн жұмыс. Энергияның сақталу заңы бойынша қималар энергияларының айырымы сұйықты қозғалысқа келтiру үшiн iстелетiн жұмыстардың айырымына тең болады: немесе

мұндағы: , - 1 мен 2 қималардағы сұйықтардың толық энергиялары.

Толық энергия кинетикалық және потенциалдық энергиялардың қосындысына тең:

, және -ның мәндерiн алғашқы формулаға апарып қойсақ, табатынымыз

Ағыстың үздiксiздiк теңдеуiнен екенiн бiлемiз, олай болса:

Екiншi жағынан,

бұл өрнектiң екi жағын да көлемге бөлсек:

Ал сұйықтың тығыздығы екенiн ескерсек:

Жалпы түрде алғанда

Бұл теңдеу Бернулли теңдеуi деп аталады.

мұндағы: - динамикалық қысым, -гидравликалық қысым, р - статикалық қысым.

Статикалық қысым (р) сұйықтың қозғалысына тәуелсiз, ал динамикалық қысым сұйық қозғалысына тәуелдi болады. Ол сұйық тежелгенде айқын бiлiнедi. Гидравликалық қысым салмақсыздық кезiнде жойылады да, асқын салмақ кезiнде өсе түседi.

Горизанталь құбыр үшiн Бернулли теңдеуi:

Сұйықтың жылдамдығы артқанда қысымы кемидi.