II. Сферическая система координат
Определим элементы фундаментальной матрицы, для этого составим скалярные произведения векторов локального базиса.
Матрица gij определена как обратная к матрице gij. Фундаментальная матрица диагонального вида, следовательно, сферическая система координат это ортогональная криволинейная система координат. Найдем векторы взаимного базиса для этой системы координат.
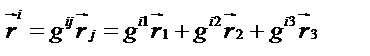
Задача 1. Известны контравариантные компоненты вектора 
в точке 
цилиндрической системы координат. Найдите ковариантные компоненты этого вектора в точке М.
Решение. Для нахождения ковариантных компонент вектора воспользуемся формулой
тогда получим
Ответ: 
Задача 2. Известны координаты вектора а в декартовой прямоугольной системе координат 
. Найдите ковариантные и контравариантные компоненты этого вектора в точке 
сферической системы координат.
Решение.
Определим векторы локального базиса в точке М сферической системы координат
Найдем ковариантные компоненты вектора в точке М, как скалярные произведения данного вектора на базисные векторы.
Найдем контравариантные компоненты вектора в точке М с помощью фундаментальной матрицы и найденных ковариантных компонент вектора.
где 
Ответ: 
