Этап 1.

ЭПЮР 1

Задача 1. определить расстояние от точки D до плоскости Г, заданной треугольником АВС.

РЕШЕНИЕ

Этап 1.

Для построения проекций точки А откладываем по оси ОХ от нулевой отметки влево координату Х точки А – ОА_Х. Через полученную точку А_Х перпендикулярно оси ОХ проводим линию проекционной связи, на которой вниз от точки А_Х откладываем координату У точки А, получаем горизонтальную проекцию А₁ точки А. Для получения фрон-тальной проекции А₂ точки А вверх от точки А_Х по линии связи откладываем координату Z точки А. Аналогично необходимо построить проекции точек В,С и D.

 

 

Этап 2. Опустить перпендикуляр из точки D на плоскость Г(АВС).

 

а) Для построения перпендикуляра сначала построим фронталь и горизонталь.

Строим фронтальную проекцию горизонтали h₂ параллельно оси ОХ.

h₂ ║ ОХ

Горизонтальную проекцию горизонтали h₁ строим по принадлежности к

плоскости Г(DАВС).

Затем строим горизонтальную проекцию фронтали f₁ параллельно оси ОХ.

f₁ ║ ОХ

Фронтальную проекцию фронтали f₂ строим по принадлежности к плоскости Г(DАВС).

 

 

 

 

 

б) Теперь из точки D опускаем перпендикуляр на фронталь и горизонталь.

Горизонтальная проекция d₁ перпендикуляра d перпендикулярна к горизонтальной проекции h₁ горизонтали h. d₁^ h₁

Фронтальную проекцию d₂ перпендикуляра d проводим под прямым углом к фронтальной проекции f₂ фронтали f. d₂ ^ f₂.

Перпендикуляр построен.

 

 

 

Этап 3. Определить точку пересечения перпендикуляра d с плоскостью Г(АВС).

Задача решается в три этапа:

а) заключаем перпендикуляр d во вспомогательную фронтально проецирующую плоскость å; d Î å;

фронтальная проекция å₂ плоскости å совпадает с фронтальной d₂ проекцией перпендикуляра d. å₂ ≡ d₂ - эта запись обязательно должна быть на чертеже;

 

 

 

 

б) определяем прямую МN по которой вспомогательная плоскость å пересекается с заданной плоскостью Г(АВС); MN = å ∩ Г;

фронтальная проекция М₂N₂ прямой МN совпадает с фронтальной проекцией å₂ вспомогательной плоскости å; М₂N₂ ≡ å₂;

горизонтальную проекцию М₁N₁ прямой МN строим по принадлежности к плоскости Г(DАВС);

 

 

 

в) определяем точку пересечения перпендикуляра d с плоскостью Г(АВС);

горизонтальная проекция К₁ точки К находится на пересечении горизонтальной проекции М₁N₁ прямой МN и горизонтальной проекции d₁ перпендикуляра d; К₁ = М₁N₁ ∩ d₁;

фронтальную проекцию К₂ точки К находим по принадлежности ее к перпендикуляру d; К₂ Î d₂.

Основание перпендикуляра точка К найдено.

 

 

 

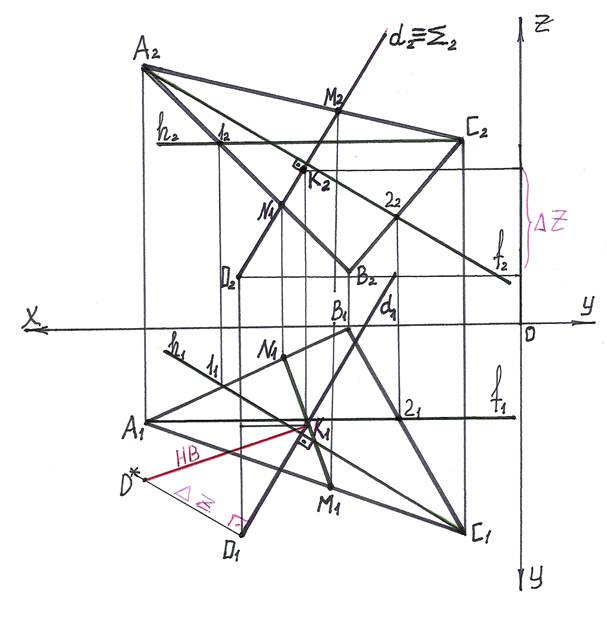
Этап 4. Определяем натуральную величину отрезка DК методом прямоугольного треугольника.

Пусть один из катетов прямоугольного треугольника есть проекция D₁К₁ отрезка DК на плоскость П₁. Второй катет строим, например, в точку D₁ перпендикулярно к D₁К₁. На полученном катете откладываем расстояние DZ, равное разности координат Z точек D и К.

Соединяем концы катетов гипотенузой – это и есть натуральная величина расстояния от точки D до плоскости Г(DАВС).

Задача решена.

 

 

ЗАДАЧА №2. Построить плоскость, параллельную заданной плоскости Г (DАВС), и отстоящую от нее на 35 мм.

 

 

 

 

РЕШЕНИЕ

 

Этап 1. Строим перпендикуляр d к плоскости Г(АВС), например в точку А.

а). Для этого сначала аналогично предыдущей задаче строим в плоскости Г фронталь и горизонталь.

Строим h₂ параллельно оси ОХ, h₁ строим по принадлежности к DАВС.

Строим f₁ параллельно оси ОХ, f₂ строим по принадлежности к DАВС.

 

 

 

 

б). Строим перпендикуляр d в точку А к плоскости Г(DАВС).

Горизонтальную проекцию d₁ перпендикуляра d строим перпендикулярно к горизонтальной проекции h₁ горизонтали h через точку А₁.

Фронтальную проекцию d₂ перпендикуляра d строим перпендикулярно к фронтальной проекции f₂ фронтали f через точку А₂.

 

 

 

Этап 2. На перпендикуляре d определим точку отстоящую на 35 мм от плоскости Г(DАВС).

а). Перпендикуляр d является прямой общего положения, поэтому сразу определить отрезок равный 35 мм невозможно.

Поставим на перпендикуляре d произвольнуюточку М, определив произвольный отрезок АМ.

 

 

 

 

б). Определим натуральную величину отрезка методом прямоугольного треугольника.

Пусть один из катетов прямоугольного треугольника проекция А₂М₂.

Под прямым углом к А₂М₂ в точку М₂ строим второй катет, на котором откладываем отрезок равный DУ. DУ – разность координат У точек А и М.

Получаем точку М^*. Соединяем концы катетов гипотенузой – это и есть натуральная величина произвольного отрезка АМ.

 

 

 

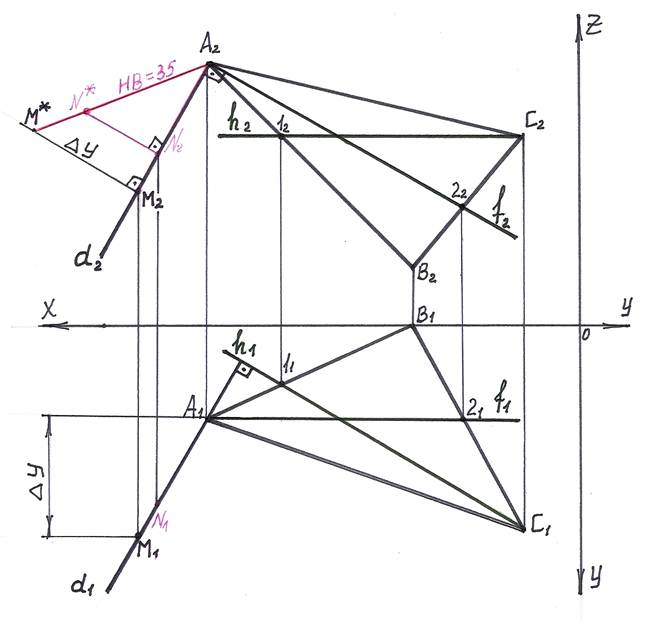
в). Продолжим (укоротим) натуральную величину до необходимых 35 мм. Определилась точка N^*. Из точки N^*опускаем перпендикуляр на проекцию А₂М₂ и

получаем точку N₂ – фронтальную проекцию искомой точки N. По принадлежности к d₁ определяем горизонтальную N₁ проекцию точки N.

Отрезок АN искомый, так как его натуральная величина по построению равна 35 мм.

 

 

Этап 3. Строим плоскость Т(а∩в) параллельную плоскости Г(АВС).

Строим а₁ ║ h₁, а₂ ║ h₂, прямая а параллельна горизонтали плоскости Г,

в₁ ║ f₁, в₂ ║ f_2, прямая в параллельна фронтали плоскости Г.

Пересекающиеся прямые а и в определяют плоскость Т.

Плоскости параллельны если две пересекающиеся прямые одной плоскости взаимно параллельны двум пересекающимся второй плоскости.

Задача решена.

Для выполнения задач эпюра 1воспользуйтесь таблицей на следующей странице.