Практическое занятие 1.1. Комплексные числа и действия над ними

Л.М. ГЕВЕЛЬ

КОМПЛЕКСНЫЕ ЧИСЛА.

ИНТЕГРАЛЬНОЕ ИСЧИСЛЕНИЕ

Учебное пособие

к практическим занятиям

Красноярск 2008

ВВЕДЕНИЕ

В настоящее время невозможно себе представить такие науки как механику, физику, химию, астрономию, но и также, экономику, биологию, медицину, языкознание без применения математики как повседневного инструмента исследований. Идет прогрессирующий процесс математизации всех наук. Этому способствует быстрое развитие вычислительной техники и её применение в различных областях.

Для решения инженерно-технических задач необходимо знание не только той науки, из которой возникла эта проблема, но и определённая математическая культура и математические познания. Поэтому, инженер в своей практической деятельности должен уметь выбирать комбинации различных известных методов и осуществлять их реализацию на ЭВМ.

Но всякие сколько-нибудь серьезные расчеты невозможно выполнить лишь при помощи средств элементарной математики.

Например, вычисление длин кривых линий, площадей фигур произвольной формы, объемов тел, ограниченных криволинейными поверхностями, нахождение центров тяжести различных тел и т.п. – все эти задачи решаются в разделе высшей математики, который называют интегральным исчислением.

Интегральное исчисление является одним из основных разделов высшей математики для студентов технических вузов и применяется при изучении общетехнических и специальных дисциплин учебного плана подготовки инженеров. Организация учебной деятельности студентов, результатом которой явилось бы усвоение раздела в полном объеме – одно из целей составления данного пособия.

Учебное пособие предназначено для проведения практических занятий. Оно содержит не только соответствующий материал стандартного курса высшей математики, но и предлагает нетрадиционное методическое осмысление общей идеи интегрального исчисления исходя из понятия меры.

В пособии приведено большое количество решенных задач и предлагаются задачи для самостоятельного решения.

Глава I. КОМПЛЕКСНЫЕ ЧИСЛА.

Неопределенный интеграл

Практическое занятие 1.1. Комплексные числа и действия над ними

1.1.1. Алгебраическая, тригонометрическая и показательная формы записи комплексного числа

Число вида: z = α + iβ называют комплексными, где – мнимая единица, при этом .

α – действительная часть комплексного числа z. Ее обозначают: α = ReZ;

β – количество мнимых единиц, или мнимая часть комплексного числа:

β = ImZ

Два комплексных числа считаются равными, если равны в отдельности их действительные и мнимые части, т.е.

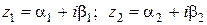
Комплексное число будет равным нулю тогда и только тогда, когда α = 0 и β = 0.

Комплексные числа 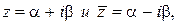отличающиеся только знаком мнимой части, называют сопряженными.

Запись комплексного числа в виде принято считать его алгебраической формой.

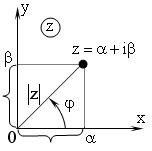
Рис. 1.1.1

Комплексные числа геометрически изображаются точками на плоскости.

Отложим на оси отрезок, равный действительной части комплексного числа – α. На оси 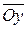- отрезок, равный числу мнимых единиц β. Точка на плоскости xOy с координатами (α,β) является геометрическим изображением комплексного числа (рис. 1.1.1).

При этом ось называют действительной осью, так как точки, лежащие на ней, соответствуют действительным числам. Последние можно рассматривать как часть комплексных, у которых β = 0.

Точки, лежащие на оси 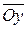, соответствуют чисто мнимым числам у которых α = 0. Поэтому ось 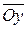получила название мнимой оси.

Соединим начало координат на комплексной плоскости с точкой (рис. 1.1.1). Получим радиус-вектор 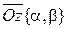. Модуль радиус-вектора или длина отрезка, соединяющего начало координат с точкой , называют модулем комплексного числа. Он равен:

Модуль комплексного числа является действительным числом.

Угол, на который нужно повернуть ось в положительном направлении (против часовой стрелки) до совпадения с радиус-вектором , называют аргументом комплексного числа, обозначают:

Очевидно, что у одного и того же комплексного числа будет бесчисленное множество аргументов. В самом деле, если к углу φ прибавить целое число оборотов, то положение точки на комплексной плоскости не изменится. Угол φ получил название главного значения аргумента комплексного числа. Его обозначают с маленькой буквы:

Все значения аргумента комплексного числа обозначают с большой буквы:

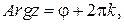где k = 0, 1, 2…

Выразим действительную и мнимую части числа через его модуль и аргумент

Подставляя значения α и β в алгебраическую форму комплексного числа, получим:

Последняя формула является тригонометрической формой комплексного числа

Выражение вида

называют показательной формой комплексного числа.

Итак, комплексное число можно представить в трех формах:

алгебраической

тригонометрической

показательной

Пример 1. Представить в алгебраической форме комплексное число

Решение. Комплексное число дано в показательной форме, его модуль , аргумент . Найдем действительную и мнимую части:

Таким образом .

Пример 2. Перейти от алгебраической к показательной форме комплексного числа z = – i.

Рис. 1.1.2

Решение. Для данного числа α =0; β = –1, найдем его модуль и аргумент:

(рис. 1.1.2)

Следовательно .

Задачи для самостоятельного решения.

Представить в алгебраической форме комплексные числа:

1. 4.

2. 5.

3. 6.

Перейти от алгебраической к триногометрической и показательной формам:

7. 10.

8. 11.

9. 12.

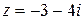
1.1.2. Действия над комплексными числами

Сложение и вычитание комплексных чисел удобнее проводить, когда они записаны в алгебраической форме, при этом их действительные и мнимые части складываются или вычитаются.

Пример 3. Найти , если ;

Рассмотрим умножение комплексных чисел в алгебраической форме.

Даны два числа:

Нужно найти произведение .

Перемножим двухчлены по правилам алгебры:

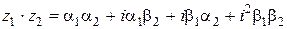если учесть, что то получим:

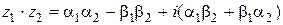Таким образом, умножение комплексных чисел в алгебраической форме проводится по обычным алгебраическим правилам.

Следует отметить, что произведение сопряженных комплексных чисел является действительным числом, в самом деле

Пусть комплексные числа даны в показательной форме

Найдем их произведение

Результат перемножения двух комплексных чисел можно записать в тригонометрической форме:

Итак, при умножении комплексных чисел в показательной и тригонометрической формах модули перемножаются, а аргументы складываются.

Деление комплексных чисел, так же как и умножение, удобнее проводить, когда они записаны в показательной или тригонометрической формах.

Найдем частное от деления двух комплексных чисел:

или

Таким образом, при делении комплексных чисел их модули делятся, а аргументы вычитаются.

Деление комплексных чисел можно проводить и в алгебраической форме.

Рассмотрим это на примере.

Пример 4. Вычислить

Решение. Умножим числитель и знаменатель на сопряженное число знаменателю 1 – i:

Такой же результат получается при переходе к показательной форме

Задачи для самостоятельного решения. Вычислить:

1. (2 + 3i) (3 – 5i);

2. (1 + 3 i) (2 + i);

3. (3 + 5 i) (3 – 5 i);

4. ;

5. .

При возведении комплексного числа в целую положительную степень в показательной или тригонометрической формах его модуль возводится в эту степень, а аргумент умножается на данную степень.

Пусть тогда

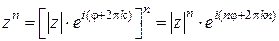или

Запишем результат возведения в целую степень в тригонометрической форме

Эту формулу называют формулой Муавра.

Пример 5. Вычислить

Решение. Перейдем к показательной форме. Найдем модуль и аргумент комплексного числа .

Задачи для самостоятельного решения. Вычислить

1. ;

2. ;

3. ;

4. .

Извлечение корня n-ой степени из комплексного числа можно рассматривать как операцию возведения комплексного числа в дробную степень т.е. .

Если комплексное число в тригонометрической форме, то

Придавая k – значения от 0 до n – 1 получим n – различных комплексных чисел, у которых модули одинаковые, а аргументы разные:

При k = 0

При k = 1

При k = 2

…………..

При k = n – 1

При k = n

Последнее значение аргумента числа совпадает с первым при k = 0.

Итак, корень n-ой степени из комплексного числа имеем n – различных значений. При вычислении значений пользуются формулами приведения:

sin (90º + x) = cos x;	;	sin (270º ± x) = – cos x;
сos (90º + x) = – sin x;	;	cos (270º ± x) = ± sin x;

и таблицей:

Таблица

Радиан
Градус		30º	45º	60º	90º
sin x
cos x
tg x					-
ctg x	-

Пример 6. Найти все значения корня .

Действительное число –1 можно рассматривать как комплексное, у которого действительная часть: α = –1, а мнимая β = 0, т.е.:

Запишем это число в тригонометрической форме. Для этого найдем его модуль и аргумент.

Рис. 1.1.3

Так как tgφ = 0 при φ = 0 и φ = π, построим число «–1» на комплексной плоскости (рис. 1.1.3), его аргумент равен

arg(–1) = φ = π = 180º

следовательно, тригонометрическая форма числа «–1» следующая:

Согласно формуле вычисления корня имеем:

Корень шестой степени имеет шесть значений, которые можно найти, если положить к равным 0, 1, 2, 3, 4, 5.

При k = 0

При k = 1

При k = 2

При k = 3

При k = 4

При k = 5

Все шесть значений корня имеют одинаковые модули и отличаются друг от друга только значением аргумента. На комплексной плоскости они расположены в вершинах правильного шестиугольника с центром в начале координат.

Задачи для самостоятельного решения. Найти все значения корня.

Практическое занятие 1.2. Неопределенный интеграл. Метод подведения под знак дифференциала. Метод замены переменной

1.2.1. Определение неопределенного интеграла и его свойства

Основной задачей дифференциального исчисления является задача нахождения дифференциала или производной данной функции, т.е. задача нахождения скорости изменения значений какой-нибудь функции, при изменении аргумента. На практике часто бывает важно решить обратную задачу: зная скорость изменения значений функции (по отношению к аргументу), найти эту функцию.

Так в механике по заданной скорости определяют закон движения материальной точки, а также закон изменения скорости (со временем) по заданному ее ускорению. Эти задачи приводят к проблеме отыскания функции по ее производной f(x). Неизвестная функция, обозначим ее F(x), получила название первообразной по отношению к своей производной.

Определение:Функцию F(x) называют первообразной для функции f(x) на числовом промежутке Х, если в любой его точке х она дифференцируема и имеет производную F'(x), равную f(x), т.е.

F '(x) = f(x).

Пример 1. Функция является первообразной для функции на интервале (–1;1), так как в любой его точке х выполняется равенство:

Пример 2. Функция – есть первообразная для функции

f(x) = cosx на интервале (–∞; ∞), ибо в каждой его точке х справедливо равенство:

(sinx)' = cosx.

Если F(x) является первообразной для функции f(x) на числовом промежутке Х, то и функция F(x) + С, где С – любая постоянная, также является первообразной для f(x) на Х. Действительно:

(F(x) + C)' = F''(x) + (C)' = F '(x) = f(x).

Следовательно, данная функция имеет бесконечное множество первообразных.

Определение. Отыскание первообразных называют неопределенным интегрированием, а выражение, охватывающее множество всех первообразных от данной функции f(x) – неопределенным интегралом от f(x) и обозначают:

где f(x) – подынтегральная функция, f(x)dx – подынтегральное выражение, х – переменная интегрирования.

Согласно данного определения, неопределенный интеграл записывают так:

, (1.2.1)

где F(x) – одна из первообразных,

F(x) + C – множество всех первообразных.