Вычисление значения функции, заданной различными аналитическими выражениями, при заданных значениях аргумента
(разветвляющийся алгоритм)
Цель работы: оставить программу для вычисления значений функции y(x); вывести на экран значения x и y(x).
Оператор условного перехода
Для программирования разветвляющегося алгоритма используется оператор условного перехода. Его общий вид:
if логическое выражение then оператор_ 1 [elseоператор_2];
Квадратные скобки означают, что конструкция elseоператор_2 может отсутствовать. Если логическое_выражение истинно, то выполняется оператор_1, иначе – оператор_2 (или следующий за ifоператор, если elseотсутствует).
Пример. Вычислим значение функции:
 |
sinx, если x£a,
y(x)= cosx, если a<x<b,
tgx , если x³b .
Указанное выражение может быть запрограммировано в виде:
if x<=a then y:=sin(x);
if (x>a)and(x<b) then y:=cos(x);
if x>=b then y:=sin(x)/cos(x);
или
if x<=a then y:=sin(x)
else if x<b then y:=cos(x)
else y:=sin(x)/cos(x); .
Варианты заданий
Значения x (по одному значению для каждого промежутка) задать самостоятельно.
1) ab-x3, если a<x<b, 2) 7(b/x-a/b)2, если x>a,
y(x)= 4(x2+a), если x³b, y(x)= 2(a-b)3(ax+bc), если x<a,
x2(a+b), если x£a; 3abx, если x=a;
a=-0.0000124; b=2/5; a=2; b=3.5; c=4.1;
 3) cos(ax2+b)2, если -19£x<-16,
y(x)= 5(bx+|a+d|), если x³-16,
2xd+a2, если x<-19;
a=-9/2; b=5.61; d=24;
|  4) a2b/9-|x|, если x£-2,
y(x)= 4(a3x2-c2), если -2<x<4,
tg[(a-b)2+x2], если x³4;
a=-0.0025; b=-2.7;c=3;
| |
5)  , если -1£x<a,
y(x) = 10(|ax|+bx), если x>a,
ax2, если x<-1;
a=21.345; b=-2/5;c=1;
| 6) x-a, если x<-1,
y(x)=  , если -1£x£1,
9x2-a, если x>1;
a=-1.5;
| |
7) 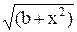 , если -2<x£3,
y(x)= ab/x-x2, если x>3,
4(x+a/b), если x£-2;
a=-0.024; b=0.752479;
| 8) 5|b-a|/(|b|-|c|)x2, если 3£x£5, y(x)= 2.5(|x|-c)(ax+b), если x<3, 102dbc/x, если x>5; a=7.4; b=2.5; c=3.1; d=0.5; | |
| 9) 5c2d2b, если x=3.5, y(x)= 4(cd2+x2), если 1.5£x<3.5, (ax+b)2, если x>3.5; a=4.7; b=2.1; c=1.7; d=0.5; | 10) 4(x/a2-a), если x<-1,
y(x)=  , если -1£x£1,
x3, если x>1;
a=12.1;
| |
| 11) x2+cos(a+bx), если x<0, y(x) = 4(x-1), если x>1, (x+2)+0.0024, если 0£x£1; a=-0.24; b=2; | 12) (a2-0.008b2)/x, если a<x£b, y(x)= bx-a, если x£a, (a+b)cosx, если x>b; a=-0.2; b=2; | |
| 13) 0.003a/x, если x£c, y(x) = 2x/a, если x³a+b, c(ax+b)2, если c<x<a+b; a=0.8; b=-0.26; c=-0.24; | 14) |a|b-x2, если x£0, y(x)= a2x+b2, если 0<x£0.1, b(x2-a2), если x>0.1; a=2/7; b=-3.01; | |
| 15) a3+dx2, если 0.1£x£a, y(x) = (b-x)2, если x>a, (b2+x2)a-x, если x<0.1; a=2.51; b=-3.06; d=5/3; | 16) x2+a, если x<a, y(x)= 8.4(x+a), если a£x£d, dx/15-ax, если x>d; a=0.2; d=1.9; | |
| 17) eax, если x<-1, y(x)= cosx+0.0085, если -1£x<0, 4x2-a, если x³0; a=29.4; | 18) (ax2+2)/(x2+1), если 1<|x|<3, y(x)= a, если |x|³3, ax/(x+2), если |x|£1; a=9/4; | |
| 19) (|a|-|b|)/(ab+x)/c, если 3<x£5, y(x)= (a-b)2x3, если 5<x<9.8, (ax2+b)/4x, если x³9.8; a=-19.2457; b=24.7; c=1.5; | 20) 4[ax-6(a+b)3], если a+b£x<a, y(x) = a2+(a-b)+x2, если x³a, x2(a+b), если x<a+b; a=2.005; b=-0.0009; | |
| 21) a2(a-b)x, если |a|<x£|b|, y(x) = 5(ax2+b), если x>|b|, (ax-|a|)2, если x£|a|; b=-1.5; a=0.6; | 22) (ab-cx)/abcx2, если x<0,
y(x)=  , если 0£x£0.8,
x2+ab, если x>0.8;
a=-5/3; b=2.3; c=-3.335;
| |
| 23) cos(x3-ab-a1/2), если a<x£b, y(x)= (x-a)3+b2, если x£a, (c+d)2+cx, если x>b; a=0.24; b=2; c=8/3; d=0.5; | 24) 9.25-|ac+dx|, если a£x£d, y(x)= 4(d2/a+c2x/b2), если x>d, ad2cx, если x<a; a=-2.3; b=5.61; c=4; d=2.5; | |
| 25) cos(ax+z), если a£x<z, y(x)= x+z+4.28, если x<a, 9(x+za), если x³z; a=-0.025; z=0.25; | ||
Задание 3: Вычислить таблицы значений функции, заданной аналитически, при ИЗВЕСТНЫХ начальном И конечном значениях АРГГУМЕНТА и шаге его изменения
(циклический алгоритм)
Цель работы: составить программу для табулирования функции y(x);
вывести на экран значения x и y(x).