В шар вписана правильная четырёхугольная пирамида, все рёбра которой равны 12см. Вычислите радиус шара.
Странно что ты не нашел решение, я уже решал эту задачу.
Диагональ основания этой пирамиды будет равна диаметру шара.
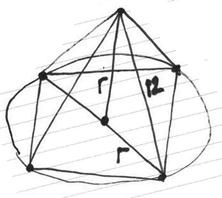
Центр шара лежит на высоте пирамиды и совпадает с центром окружности, вписанной в квадрат.
144=2r2
r=6√2
В конусе даны радиус основания R и высота H. Найдите ребро вписанного в него куба
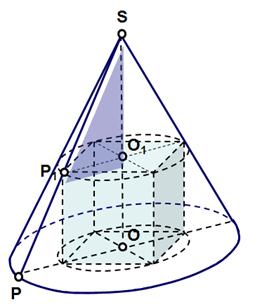
OP=R
SO=H
O1P1=a, сторона куба вписанного в конус радиусом R и высотой H
По подобию треугольников POS и P1O1S
H /SO1 = R / P1O1
SO1=H-a
P1O1 = a/√2. Является половиной диагонали основания куба и найдется так потому что угол у пересечения диагоналей равен 90 градусов.
Теперь запишем это все как соотношение:
H/(H-a)=R/(a/√2)
Отсюда:
Ha/√2 = RH – Ra
Образующ. конуса 13 см, высота 12 см. Конус пересечен прямой, параллельной основанию; расстояние от нее до основания равно 6 см, а до высоты 2 см. Найдите отрезок этой прямой, заключенной внутри конуса.
Радиус основания конуса равен 5, это стоит запомнить так как еще одна тройка Пифагора 5-12-13.

O1S1=Rкон
По подобию k=SO1/SO=2, следовательно OS=R/2=2.5
2.52-22=a2, где a - длина нашего отрезка.
Через точку О, лежащую между параллельными плоскостями альфа и бета, проведены прямые к и м. Прямая к пересекает плоскости альфа и бета в точках А1 и А2 соответственно, прямая м - в точках В1 и В2. Найдите длину отрезка А2В2, если А1В1=12 см,В1О:ОВ2=3:4

Тут все очень просто если вы знаете что они параллельны, ну плоскости, получается углы B2OA2 и B1OA1 равны между собой. А стороны A1B1 и A2B2 параллельны. Значит треугольники подобные и следовательно относиться стороны будут между собой
В1О:ОВ2 = A1B1/A2B2 = 3/4
12/x = 3/4
x=4*12/3=16
В тетраэдре ДАВС угол ДВА=углуДВС=90 градусов, ДВ=6,АВ=ВС=8,АС=12. Постройте сечение тетраэдра плоскостью, проходящей через середину ДВ и параллельно плоскости АДС. Найдите площадь сечения.

Практические идентичная задача, только тут всего лишь трудность построить такое сечение. Для начала выделите основные моменты. Именно в этой задаче еще раз придется вернуться к коэффициенту подобия k, который найдется из частного сторон подобных фигур. В общем это писалось неоднократно, и формулы простейшие.
A1B1 - является средней линией равнобедренного треугольника ABC. Плоскости построенные на треугольниках ABД и A1B1Д1 параллельны.
Следовательно треугольники ABД и A1B1Д1 подобные и притом все стороны A1B1Д1 вдвое меньше сторон ABД.
Получается что Д1B1=ДB/2=3
A1B1=8/2=4
S(ΔA1B1Д1)=3*4/2=6
Все грани параллелепипеда АВСДА1В1С1Д1 прямоугольники, АД=4,ДС=8,СС1=6. Через середину ребра ДС параллельно плоскости АВ1С1 проведена плоскость .Найдите периметр сечения.

5*4=20