Стороны оснований правильной усеченной треугольной пирамиды 4 и 12 дм. боковая грань образует с большим основанием угол 60 градусов. Найдите высоту.

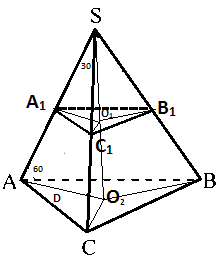
В пирамиде ABCS построим еще пирамиду A1B1C1S

Так как пирамида правильная следует полагать что плоскости построенные на треугольниках ABC и A1B1C1 параллельны. А значит что пирамида ABCS подобна A1B1C1S.

Тут идея простая если ∠BAC=∠ABS=60 градусов, то тогда получается что боковые грани AS,BS,CS пирамиды ABCS равны AB,BC,CA=12 дм.

То же самое могу сказать про пирамиду A1B1C1S. Нам точно известно что A1B1,B1C1,C1A1=4 дм. (но это не понадобится)

Итак для того чтобы найти высоту пирамиды ABCS - SO2 нужно обратить внимание на прямоугольный треугольник AO2S.

∠SAO2=60, а значит что угол ASO2=30. А напротив угла 30 градусов лежит сторона равная половине гипотенузы.

AO2=12/2=6

Значит высота AO2 пирамиды ABCS = √(144-36)=√9*4*3=6√3

Теперь на чем основывается принцип подобия фигур?

Если у нас пирамида ABCS подобная A1B1C1S имеет высоту равную 6√3, то другая будет иметь высоту во столько раз меньше, во сколько относятся стороны этих пирамид.

Иначе говоря найдем коэффициент подобия фигур

k=12/4=3

Значит что высота O1S=(6√3)/3=2√3

Получается что O1O2=6√3-2√3=4

 

 

Основанием пирамиды SABC служит треугольник, у которого АВ=ВС=20 с, АС=32 см; углы между плоскостью основания и каждой из боковых граней равны 45 (градусов). Найдите объем пирамиды

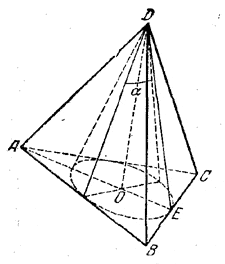
Пусть дана пирамида ABCD. В основание впишем окружность и найдем OE. ∠EOD=90, ∠OED=∠EDO=45 отсюда следует найдем EO найдем и высоту пирамиды.

EO=Rвпис.окр=Sосн/p, где p - полупериметр. p=(40+32)/2=36

DO=Sосн/36

Потом по формуле V=(Sосн)2/3

Найдем площадь основания по формуле Sосн=a*h, где a-AC, h=12 (Правило идеальных треугольников в принципе если непонятно просто проведи высоту к стороне AC, затем найди эту высоту по формуле Пифагора, просто облегчают такие цифры решение как 20-16-12, 10-8-6, 5-4-3 это все треугольники прямоугольные с такими сторонами запутал наверное).

Sосн=32*12=384

V=384*384/3=49152