Площадь равнобедренного прямоугольного треугольника равна 36. Найти длину гипотенузы
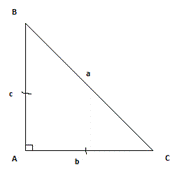
Пусть ABC равнобедренного прямоугольный треугольник, у которого катеты равны, так как гипотенуза не может быть равна катету.
Получается что площадь такого треугольника можно найти по формуле c*b/2, так как c=b по условию, то найдем катеты:
с2=36*2
с=6√2
Тогда гипотенуза равна: a2=2*с2
a2=2*36*2=4*36
a=2*6=12 см
Из всех правильных треугольных призм, имеющих объем ν найдите призму с наименьшей суммой длин всех ее ребер . чему равна длина стороны основания этой призмы.
Правильная треугольная призма, представляет собой призму в основании которой лежит правильный треугольник, всего у этой призмы три ребра.
Начнем с того, как найти объем такой призмы.
Vпр=Sосн*H. В нашем случае H равна ребру, так как призма не наклонная, а прямая.
Sосн=Vпр/H
Sосн=a2•√(3)/4, здесь a длина стороны равностороннего треугольника при основании.
a2=4Sосн/√(3)=4Vпр/√(3)*H
Точки А, В, С, D не лежат в одной плоскости. Докажите что любые 3 из них не лежат в одной плоскости
Если любые три будут лежать в одной плоскости то первое утверждение А, В, С, D не лежат в одной плоскости не верно. На трех точках построить можно плоскость!