Объем прямоугольного параллелепипеда равен 2520 см(в кубе),а площадь основания 168 см(в квадрате),и длина на 2 см больше ширины. Найдите сумму длин всех ребер параллелепипеда.
Даже рисунок не понадобится, потому что решается устно.
Итак что такое объем параллелепипеда? Vпар=Sосн*H, где H одно из наших ребер и их всего 4. Покажу на рисунке позже.
H=2520/168=15 см.
Итак мы нашли одно ребро. осталось остальные два, которые получаются их основания.
Sосн=a*b; где a,b - стороны основания параллелепипеда.
Известно что a=b+2
Значит верным будет:
b*(b+2)=168
b2+2b-168=0
Решение квадратных уравнений, быстро и просто.
Ответ: b1 = 12; b2 = -14 (не может быть так как отрицательное)
Отсюда b=12; a=12+2=14
Теперь рисунок.
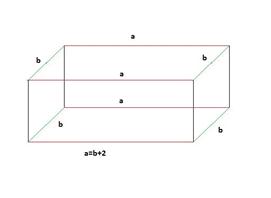
Для наглядности, я специально обозначил ребра равные a красным цветом. Ребра b зеленым, а высота H осталась черным.
Получается что всего в параллелепипеде по 4 каждого ребра. То есть логично записать что сумма будет равна:
P=4*(a+b+H)=4*(12+14+15)=41*4=164
Площадь основания пирамиды равна 108 дм2, а ее высота — 24 дм. Сечения пирамиды, параллельные плоскости основания, имеют площади 48 и 75 дм3. Найдите расстояние между плоскостями сечений.

Итак мы имеет пирамиду ABCS (нарисовал треугольную, потому что в этом задании нет разницы)
Начертим также два сечения DFE и D1F1E1 параллельные плоскости ABC.
Теперь мы видим что у нас получились подобные пирамиды. Давай разберем по порядку:
1) Пирамида DFES будет подобна пирамиде ABCS. Согласно правилу подобия площадей S(ΔABC)/S(ΔDFE)=k2
Найдя коэффициент подобия, мы сможем найти высоту пирамиды DFES.
108/48=2,25 → k=√(2,25)=1.5
Теперь вспомним, что высоты, стороны у подобных фигур в отношении получают k=h1/h2
Итак наша высота равна 24/h(DFES)=1.5 → h(DFES)=24/1.5=16
2) Точно также пирамида D1F1E1S подобна ABCS. Найдем ее высоту, таким же способом.
k=√(108/75)=1.2
24/h(D1F1E1S)=1.2 → h(D1F1E1S)=24/1.2=20
3) Нам нужно расстояние от плоскости DFE до D1F1E1. Оно будет равно 20-16=4 дм.
Основание пирамиды — равнобедренный треугольник с углом при вершине α и радиусом описанной окружности R. Две неравные боковые грани перпендикулярны плоскости основания, а третья грань наклонена к ней под углом β. Найдите боковую поверхность пирамиды.

На рисунке показана пирамида ABCS, из вершины S пр ведена апофема SK на AC равнобедренного треугольника при основании. Все это нам потребуется для решения данной задачи.
Итак радиус описаной окружности может быть найден как:
R=a/2sinα → CB=a=R*2sinα
Теперь зная сторону CB найдем остальные стороны AC и AB, которые равны между собой.
∠ABC=∠ACB=(180-α)/2
AC=AB=R*2sin[(π-α)/2]
Давай запишем какие площади составляют боковую поверхность:
Sбок.пов.=S(ΔACS)+S(ΔBCS)+S(ΔABS)
Теперь нужно расписать как найти каждую из них.
S(ΔACS)=SK*AC
S(ΔBCS)=AB*BS/2
S(ΔABS)=CB*BS/2
В правильной треугольной пирамиде отрезок, соединяющий основание высоты пирамиды с серединой апофемы, равен m и образует с высотой пирамиды, угол β. Найдите полную поверхность пирамиды.

На рисунке изображена пирамида ACBO, OM-высота, OK-Апофема.
Точка L середина апофемы OK, LM образует с высотой OM угол β.
ΔOMK прямоугольный, следовательно ML является медианой этого треугольника, значит OL = LM = LK = m
OK=2m
ΔOLM равнобедренный, следовательно ∠OML = ∠LOM, а это значит что апофема образует с высотой угол β (на рисунке показано).
Sосн=3*r2*√(3)
Sбок=p•a/2; где p - полупериметр основания, a - апофема OK.
В основании нашей пирамиды лежит правильный треугольник, стороны которого равны. Найдем сторону основания, для этого воспользуемся уже имеющимися данными. Как известно MK является радиусом вписанной в основание окружности.
r=AB*√(3)/6 → AB=6r/√(3)
Найдем чему равен r, зная что sinβ=MK/OK →OK=MK/sinβ=2m/sinβ
Sосн=(2m/sinβ)2*3*√(3)
AB=6*2m/sinβ*√(3)=12m/sinβ*√(3)
p=3*12m/sinβ*√(3)=36m/sinβ*√(3)
Sбок=36m*2m/sinβ*√(3)
Sполн=[72m2/sinβ*√(3)]+(2m/sinβ)2*3*√(3)