Дано прямая четырехугольная пирамида. Диагональ основание 10см. боковое ребро 13 см. Найдите высоту пирамиды.

Получается что у нас есть равнобедренный треугольник. Площадь его равна: √(p(p-a)(p-b)(p-c)), где p полупериметр равный 13+13+10=18 см.

Теперь объясню зачем нам площадь такого треугольника понадобилась, дело в том что высоту можно будет найти исходя из формулы SΔ=a*h, где a - основание.

√(p(p-a)(p-b)(p-c))=a*h

√(18(18-10)(18-13)(18-13))=10*H

H=60/10=6 см

 

 

Основание пирамиды треугольник с катетами 6 и 8см. угол между боковой поверхностью и основанием составляет 60 градусов. Найдите высоту пирамиды.

 

В основании этой пирамиды лежит прямоугольный треугольник. Найдем гипотенузу - √(6*6+8*8)=10 см.

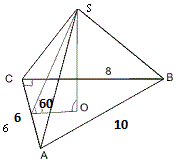
Боковые грани одинаково наклонены к плоскости основания на угол 60 градусов, апофемы боковых граней равны, а это значит что основание высоты совпадает с центром вписанной окружности.

Найдем радиус вписанной окружности а прямоугольный треугольник по формуле, можете записать пригодится: r= (a+b-c)/2, где a и b - катеты, c - гипотенуза.

r=(6+8-10)/2=2 (один из катетов образованных прямоуг. треугольником с высотой h)

Напротив угла 30 лежит сторона в 2 раза меньшая гипотенузе. Следовательно высота будет равна:

h=√(4*4-2*2)=√12