Р лежит в плоскости трапеции АВСD. АD параллельна ВС. Доказать, что прямая, проходящая через середины РВ и РС параллельна Средней линии трапеции.

Для начала вспомним что такое средняя линия, это линия которая соединяет половоны отрезков AB и DC. На рисунке я показал среднюю линию пунктиром.

Теперь мы поставили точку и провели линии к B и C. Получился треугольник, в котором половины сторон РВ и РС будут образовывать линию параллельную ВС, а как мы знаем средняя линия параллельна ВС, а значит и нашей прямой.

точка P на рисунке лежит внутри трапеции, но если мы ее нарисуем за ее пределами, от этого не изменится решение!

 

 

Середины сторон CD и BD треугольника BCD лежат в плоскости (альфа) а сторона ВС не лежит в этой плоскости. Докажите что прямая ВС и альфа параллельны.

 

Прямая на рисунке C1B1 является средней линией треугольника BCD которая параллельна стороне CB. Если прямая СB паралельна прямой лежащей на плоскости альфа, то она будет параллельна самой плоскости.

 

 

Основанием пирамиды является равносторонний треугольник, сторона которого равна 12 см. Каждое боковое ребро пирамиды образует с плоскостью основания угол 45 градусов. Найдите высоту пирамиды

 

 

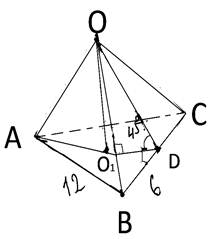
ABC - равносторонний треугольник. BD является высотой равностороннего треугольника.

Высота O1O, опущенная из вершины на основание ABC, падает в центр вписанного в основание круга.

Если подумать то O1O = OD, так как угол OO1D равен 90 градусов, а угол O1DO равен 45 градусам.

Найдем радиус вписанной окружности по формуле [√(3) * AB ]/6

[√(3)*12]/6=2√3

 

 

Основание пирамиды - ромб с диагоналями 6 м и 8 м, высота пирамиды проходит через точку пересечения диагоналей ромба и равна 1 м. Найдите боковую поверхность пирамиды.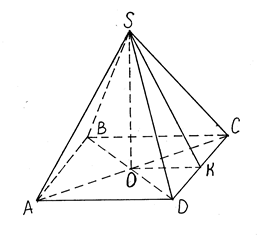

На рисунке представлена пирамида ABCDS где S является вершиной и высота падает в центр O пересечения диагоналей основания ABCD. SK является апофемой.

Для того чтобы найти площадь боковой поверхности необходимо сложить площади ΔABS, ΔADS, ΔDCS, ΔBCS.

ΔABS=ΔDCS=ΔADS=ΔBCS, это следует из того что пирамида правильная, высота падает в центр пересечения диагоналей AC и BD, а стороны основания равны!

Сначала найдем сторону основания ABCD, для этого вспомним что в ромбе половины диагоналей образуют прямоугольный треугольник. Отсюда AB=BC=DC=AD=√(42+32)=5 см.

Так как треугольники ΔABS=ΔDCS=ΔADS=ΔBCS равны, то достаточно найти площадь одного из них и умножить все на 4.

S(ΔDCS)=SK*DC=5*SK

SK2=SO2+OK2

Точка K является центром описанной окружности вокруг треугольника COD. OK=радиусу этой окружности, и находится по формуле:

S(ΔCOD)=3*4/2=6

OK=R=CO*OD*DC/4*S(ΔCOD)=4*3*5/4*6=60/24=2.5

SK2=12+2.52=1+6.25=7.25

SK=√7,25

S(ΔDCS)=SK*DC=5*√7,25

Sбок=5*4*√7,25=20*√7,25