Около куба описан цилиндр. найти полную поверхность цилиндра, если поверхность куба равна S
Задачи с решениями по геометрии
Шар, радиус которого 13см пересечен плоскостью на расстоянии 12см от центра. Найдите площадь сечения
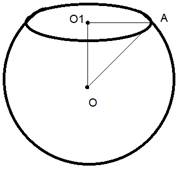
Пусть точка O центр шара, а точка O1 центр окружности отсекаемой плоскостью альфа, следовательно O1X радиус окружности.
Найдем этот радиус по теореме Пифагора:
O1X2=OX2-O1O2
O1X2=132-122=25
O1X=r=5
Sсеч=25п
Периметр правильного треугольника, вписанного в окружность, равен 54 см. Найдите периметр квадрата, вписанного в эту окружность.
Радиус описанной окружности около правильного треугольника
rокр=√3*a/3, где a-сторона треугольника.
54/3=18
rокр=√3*18/3=6√3
Следовательно сторона квадрата будет равна: b2+b2=(6√3)2
2b2=36*3
b2=54
b=√54=3√6
P=4*3√6=12√6
Найдите боковую поверхность цилиндра с высотой, равной 3см, если осевое сечение цилиндра плоскостью-квадрат
В основании этого цилиндра лежит окружность с диаметром 3 см, это следует из условия "осевое сечение цилиндра плоскостью-квадрат"
Для того чтобы найти боковую поверхность цилиндра надо длину окружности что лежит в основании умножить на высоту!
Теперь остается лишь подставить: Sбок=3*п*3=9п
Около куба описан цилиндр. найти полную поверхность цилиндра, если поверхность куба равна S
Чтобы решить это задание, нужно знать формулу полной поверхности цилиндра:
Sполн=Sосн*2+Sбок.пов.
Для того чтобы найти Sосн=пR2; а Sбок.пов.=H*2пR, где H-высота цилиндра, R-радиус основания цилиндра, п-величина "пи"=3,14....
Наш цилиндр описан около куба, следовательно его длина его ребра равна высоте нашего цилиндра, а радиус равен √2a2=a√2 (Из правила прямоугольного треугольника)
В дано нам дается только площадь поверхности нашего куба, которая равна Sкуба=6a2, отсюда a2=S/6
Теперь запишем вместе формулу полной поверхности цилиндра и начнем упрощать.
Sполн=пR2*2+H*2пR=2пR(R+H)
Теперь просто подставим значения R и Н
Sполн=2п*a√2(a√2+a)=2п(2a2+a2√2)
Подставим a2=S/6 Sполн=2п(2S/6)+2п(√2S/6)=(2пS/3)+(√2пS/3)=(2пS+√2пS)/3
Дальше смотрите по ответу, я точно преобразить не смогу, потому что не знаю в каком виде дают ответы в тесте, но в принципе формула остается такой
Длина бокового ребра правильной треугольной пирамиды равна √3 см.
Боковое ребро составляет с плоскостью основания угол 60°. Найти радиус описанного около пирамиды шара.
Начертим вот такой рисунок, чтобы было все понятно напишу ниже что к чему.
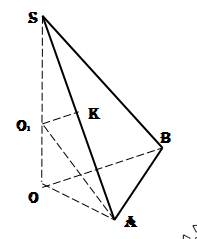
SA - боковое ребро, обозначим его буквой b (В нашем случае равна √3)
∠SAO - угол наклона ребра к плоскости основания, обозначим буквой α (Равен 60°)
SO - высота пирамиды, SO=H
S01 - радиус описанного шара SO1=R
Так как центр описанного шара O1 - точка пересечения плоскостей, проведённых через середины ребёр, перпендикулярно к ним, то есть SK=KA; O1K⊥SA
∠SO1K=∠SAO как углы с соответственно перпендикулярными сторонами, SA=2SK
Из ΔO1SK: SK=O1S*sin∠SO1K ⇒ SA=2O1S*sin∠SO1K
∠SO1K=∠SAO, поэтому ∠SO1K=α ⇒ b=2R*sinα (Запиши эту формулу, называется уравнением связи и применима только если пирамида правильная, т.е. ребра наклонены к основанию под одним углом или они равны между собой)
Решая теперь твою задачу найдем R:
R=b/2*sinα=√3/2*sin60°=√3/2*(√3/2)=1
Существует еще одно уравнение связи:
ΔSO1K~ΔSOA (∠SO1K=∠SAO, ∠SKO1=∠SOA=90°) ⇒ SO/SA=SK/SO1 ⇒ H/b=b/2R
b2=2HR (Уравнение связи второе, пригод