Моменты инерции некоторых тел

 

Обратим внимание, что тело обладает моментом инерции безотносительно к вращению. Как покоящееся тело обладает массой, так же оно обладает и моментом инерции. Наличие массы проявляется при поступательном движении, а наличие момента инерции при его вращении. Величина момента инерции зависит от расположения элементарных масс относительно оси вращения. Следовательно, момент инерции можно представить в виде:

. (2.9.1)

Осуществляя предельный переход, получаем, что задача вычисления момента инерции, сводится к интегрированию по всему объему тела:

, (2.9.2)

где величины r и являются функциями координат.

Очевидно, что вычисление моментов инерции представляет собой сложную задачу, особенно в тех случаях, когда тело неоднородно и имеет неправильную форму. Приемы вычисления моментов инерции некоторых тел проиллюстрируем на следующих простых примерах.

Пример. Пусть имеется тонкий однородный стержень массой 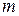и длинной . Вычислим момент инерции относительно оси, перпендикулярной стержню и проходящей через его центр масс (рис. 2.9).

Рис. 2.9. К определению момента инерции однородного стержня
относительно оси вращения, проходящей через его центр

Разделим стержень на малые элементы объемом , каждый из которых обладает массой .

Момент инерции всего стержня относительно оси по определению (3.9.2) равен

.

Пример. Пусть теперь ось проходит через конец стержня A параллельно оси . Вычислим момент инерции стержня относительно
этой оси.

В этом случае изменяются пределы интегрирования, и мы имеем:

.

Пример. Пусть теперь имеется стержень, плотность которого меняется по закону , где — плотность стержня в точке A.

В этом случае путем прямого вычисления найдем момент инерции стержня относительно оси, перпендикулярной стержню и проходящей через точку A:

.

Простые вычисления приводят к следующему результату:

,

где .

Мы показали, что момент инерции одного и того же тела будет разным относительно разных осей вращения.

Относительно легко вычисляются моменты инерции тел, имеющих оси симметрии. Если симметричное однородное тело вращается вокруг вертикальной оси, то силы бокового давления на ось не возникают. Если бы отсутствовали силы тяжести, то подшипники можно было бы и убрать, при этом ось сохраняла бы свое положение в пространстве.

Ось, которая сохраняет в пространстве свое положение неизменным, при вращении тела вокруг нее, называется свободной осью.

В механике доказывается, что для тела любой формы и с произвольным распределением массы существуют три взаимно перпендикулярные оси, проходящие через центр масс, которые могут служить свободными осями. Такие оси называются главными осями инерции. Моменты инерции тела относительно главных осей инерции называются главными моментами инерции тела. В общем случае эти моменты инерции различны. В случае тела, обладающего центральной симметрией, все три главных момента инерции одинаковы. Это, например, справедливо для однородного шара, куба и т. п. В качестве примеров приведем значения главных моментов инерции некоторых однородных тел простейшей формы и проанализируем зависимость этих значений от геометрических параметров тел. Знание главных моментов инерции очень важно с практической точки зрения. Это обусловлено тем, что ось вращения, проходя через центр масс, необязательно направлена вдоль одной из главных осей. Можно доказать, что момент инерции всякого тела, вычисленный относительно любой оси, проходящей через центр масс, связан с главными моментами инерции следующим соотношением:

где — углы, образованные данной осью с осями , направленными вдоль главных осей инерции.

1. Полый круглый цилиндр высотой и радиусами внешней и внутренней поверхностей , соответственно (рис. 2.10).

Рис. 2.10. К определению моментов инерции полого цилиндра
относительно осей координат

,

.

Если цилиндр является сплошным, т. е. , , то имеем: , .

Замечательным свойством сплошного цилиндра является независимость момента инерции от его высоты. Если высота цилиндра достаточно велика, то цилиндр вырождается в стержень цилиндрической формы. Если то с точностью до 1 %

Если высота цилиндра мала, то он вырождается в диск. Моменты инерции и равны

Если цилиндр тонкостенный , то , . Если , то цилиндр вырождается в кольцо и его момент инерции относительно любого диаметра равен .

3. Полый шар с радиусами внешней и внутренней поверхностей равными и соответственно (рис. 2.11).

Рис. 2.11. К определению моментов инерции полого шара
относительно осей координат

.

Для сплошного шара , , .

Для тонкостенной сферы , .

Для однородного шара или сферической поверхности моменты инерции относительно любой оси, проходящей через центр, будут одинаковы.