Графическое отделение корней

 

Графическое отделение корнейосновано на графическом способе решения уравнений – отыскании точек, в которых функция f(x)пересекает ось 0Х.

 

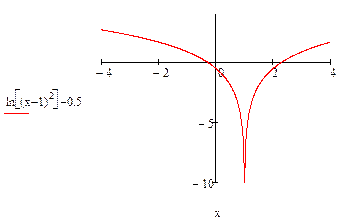
Пример 6.2.2-1. Отделить корни уравнения ln (x-1)² – 0.5 = 0.

На рис. 6.2.2-1 изображен график функции y = ln (x-1)² – 0.5, из которого следует, что уравнение имеет два действительных корня 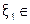[-1;0] и [2;3].

 

Рис.6.2.2-1

 

В некоторых случаях удобно вначале преобразовать функцию f(x) к виду f(x)=g₁(x)- g₂(x), из которого, при условии f(x)=0, следует, что g₁(x)=g₂(x). При построении графиков y₁=g₁(x)и y₂=g₂(x)находят отрезки, содержащие точки пересечения этих графиков.

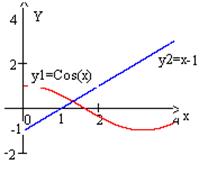
Пример 6.2.2-2. Отделить корни уравнения сos(x) – x + 1 = 0.

Приведем исходное уравнение к виду сos(x)= x – 1. Построив графики функций y₁ = сos(x) и y₂ = х – 1 (рис. 6.2.2), выделим отрезок, содержащий корень 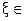[1;2].

 

Рис. 6.2.2-2