Метод сечений. Поверхности вращения
Литература: [1], гл.15, §1, 8, стр. 364–368, 390-393; [2], гл. 4, § 1,5,
стр. 116–119, 132-140; [27], гл.9, § 74-75, стр. 257-262.
Основные определения, теоремы и формулы
Поверхность, которая вместе с каждой своей точкой содержит всю окружность, полученную вращением этой точки вокруг некоторой фиксированной прямой 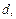 называется поверхностью вращения. Прямая
называется поверхностью вращения. Прямая 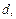 вокруг которой производится вращение, называется осью вращения.
вокруг которой производится вращение, называется осью вращения.
Теорема. В прямоугольной системе координат уравнение
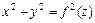
есть уравнение поверхности вращения, образованной вращением вокруг оси 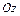 линии, заданной уравнениями
линии, заданной уравнениями 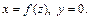
Вопросы для самоконтроля
1. Что называется уравнением поверхности?
2. Какие поверхности называются алгебраическими?
3. Что такое порядок алгебраической поверхности?
4. Зависят ли понятие и порядок алгебраической поверхности от выбора аффинной системы координат?
5. Что называется поверхностью второго порядка?
6. Привести примеры алгебраических и неалгебраических поверхностей.
7. Является ли алгебраической поверхностью поверхность, заданная в аффинной системе координат уравнением:
а) x2 + y2 + z2 – 4sin2(x + y + z) – 4cos2(x + y + z) = 0;
б) 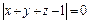 ;
;
в) (x + y + z)n = 0, где n – некоторое натуральное число;
г) 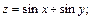
д) 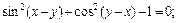
е) 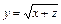 ;
;
ж) x = 1;
з) 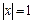 ;
;
и) y2 = 2px.
8. В чем состоит сущность метода сечений? Будет ли верным утверждение, если в теореме из [1, стр. 217], прямоугольную систему координат заменить на произвольную аффинную систему координат?
9. Какой вид имеют уравнения проекции на плоскость Охz (Оуz) линии пересечения поверхности, заданной уравнением F (х, у, z) = 0, с плоскостью, параллельной плоскостям Охz (Oyz) или совпадающей с ней? Написать соответствующие уравнения для других координатных плоскостей.
10. Что называется поверхностью вращения? Является ли ось вращения d осью симметрии, а плоскость, проходящая через d, – плоскостью симметрии поверхности вращения?
11. Может ли поверхность вращения иметь более чем одну ось вращения?
12. Верно ли утверждение: “любая поверхность, имеющая ось симметрии, является поверхностью вращения”?
13. Как записывается в прямоугольной декартовой системе координат Охуz уравнение поверхности, образованной вращением вокруг оси Оz линии, заданной уравнениями 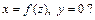 Сформулировать аналогичную теорему об уравнении поверхности вращения, если ось вращения
Сформулировать аналогичную теорему об уравнении поверхности вращения, если ось вращения 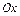
14. Даны две прямые а, b, лежащие в одной плоскости. Что представляет собой поверхность, образованная вращением прямой а вокруг прямой b?
15. Верно ли утверждение, что поверхность вращения, имеющая две пересекающиеся взаимно перпендикулярные оси вращения, имеет:
а) центр симметрии, б) еще одну ось вращения, в) бесконечно много осей вращения? Что это за поверхность?
Пример. Составить уравнение поверхности, образованной вращением параболы, заданной системой 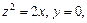 вокруг оси Оz.
вокруг оси Оz.
Решение. Запишем уравнение параболы в виде 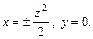 Тогда по сформулированной выше теореме искомое уравнение поверхности вращения имеет вид
Тогда по сформулированной выше теореме искомое уравнение поверхности вращения имеет вид
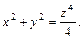
Задачи
1. Написать уравнение поверхности вращения, образованной вращением вокруг оси 0х (оси 0y) линии, заданной уравнениями:
а) 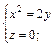 б)
б) 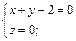 в)
в) 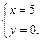
2. Доказать, что поверхности, заданные следующими уравнениями являются поверхностями вращения:
а) x2 – y2 + z2 = 0, б) x2 + y2 = 4, в) x4 + 2x2y2 + y4 + x2 + y2 + z = 0.
Найти образующую линию и ось вращения каждой поверхности.
3. Дана поверхность x2 + y2 – 2z2 = 1. Найти линии её пересечения с координатными плоскостями и плоскостями, им параллельными и проходящими от них на расстоянии 1 по обе стороны. Изобразить проекции этих сечений на соответствующие координатные плоскости.
4. Исследовать методом сечений поверхности второго порядка:
а) x2 + y2 – 2y = 0, б) x2 – 2x – 2y + 1 = 0.
5. Напишите уравнение поверхности, образованной вращением:
а) эллипса 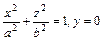 вокруг оси Ox,
вокруг оси Ox,
б) гиперболы 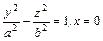 вокруг оси Oz,
вокруг оси Oz,
в) параболы 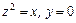 вокруг оси Oz (вокруг оси Ox).
вокруг оси Oz (вокруг оси Ox).
Домашнее задание
1. В плоскости Oyz дана окружность с центром в точке (0,4,0) радиуса 1. Написать уравнение поверхности, образованной вращением данной окружности вокруг оси Oz.
2. Написать уравнение поверхности, образованной вращением параболы, заданной уравнениями z2 = 10y, x = 0, вокруг оси Oz.
3. Доказать, что поверхность, заданная уравнением, является поверхностью вращения:
а) 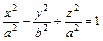 ,
,
б) 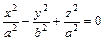 .
.
4. Выяснить, можно ли через точку 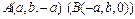 этой поверхности провести прямую, каждая точка которой принадлежит этой поверхности?
этой поверхности провести прямую, каждая точка которой принадлежит этой поверхности?
5. Определить вид сечения однополосного гиперболоида, заданного уравнением, плоскостью, проведенной через точку (0, 0, 1) параллельно плоскости Оху.
6. Исследовать методом сечений поверхность, заданную уравнением x2 + 2y2 - 4z2 – 8z = 8.
Задачи повышенной трудности
1. Написать уравнение поверхности, образованной вращением параболы с фокальным параметром 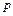 вокруг ее директрисы, если парабола лежит в плоскости
вокруг ее директрисы, если парабола лежит в плоскости 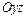 , симметрична относительно оси ординат, а ее директриса совпадает с осью вращения
, симметрична относительно оси ординат, а ее директриса совпадает с осью вращения 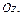
2. Линия 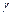 в пространстве задана уравнениями
в пространстве задана уравнениями 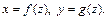 Доказать, что поверхность, образованная вращением
Доказать, что поверхность, образованная вращением 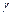 вокруг оси
вокруг оси 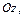 имеет уравнение
имеет уравнение 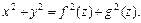
Тема 2.8. Цилиндрические и конические поверхности
Литература: [1], гл.15, § 8, стр. 385–390, гл. 18, § 2, 3, стр. 478–482; [2], гл. 4, §5, стр. 132–140; гл. 7, § 2, 3, стр. 197–201; [27], гл.9, §76-77, стр. 262-271.
Основные определения, теоремы и формулы
Поверхность, обладающая тем свойством, что вместе с каждой точкой 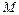 она содержит всю прямую, проходящую через точку
она содержит всю прямую, проходящую через точку 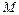 , параллельную данному ненулевому вектору
, параллельную данному ненулевому вектору  называется цилиндрической поверхностью или цилиндром. Прямые, параллельные вектору
называется цилиндрической поверхностью или цилиндром. Прямые, параллельные вектору  и принадлежащие цилиндрической поверхности, называются образующими этой поверхности.
и принадлежащие цилиндрической поверхности, называются образующими этой поверхности.
Теорема. Пусть в пространстве дана прямоугольная система координат 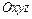 и в плоскости
и в плоскости 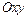 задана линия
задана линия 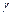 своим уравнением
своим уравнением 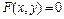 . Тогда уравнение
. Тогда уравнение 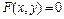 в пространстве определяет цилиндрическую поверхность с направляющей линией
в пространстве определяет цилиндрическую поверхность с направляющей линией 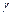 и образующими, параллельными оси
и образующими, параллельными оси 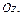
Например, на плоскости 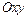 уравнение
уравнение 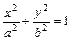 определяет эллипс, а в пространстве – это уравнение эллиптического цилиндра.
определяет эллипс, а в пространстве – это уравнение эллиптического цилиндра.
Конической поверхностью или конусом с вершиной в точке  называется поверхность, которая обладает тем свойством, что вместе с каждой своей точкой
называется поверхность, которая обладает тем свойством, что вместе с каждой своей точкой 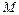 , отличной от точки
, отличной от точки  , эта поверхность содержит прямую
, эта поверхность содержит прямую 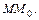 Прямые, проходящие через вершину конуса и лежащие на нем, называются образующими этого конуса.
Прямые, проходящие через вершину конуса и лежащие на нем, называются образующими этого конуса.
Уравнение конической поверхности с вершиной в начале координат, направляющей которой служит эллипс, заданный уравнениями
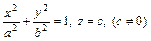 имеет вид
имеет вид 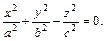
Пример. Написать уравнение цилиндрической поверхности, образующие которой параллельны вектору 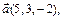 если его направляющая задана уравнениями
если его направляющая задана уравнениями 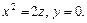
Решение. Пусть  произвольная точка искомой поверхности
произвольная точка искомой поверхности 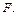 По определению цилиндрической поверхности существует образующая
По определению цилиндрической поверхности существует образующая 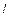 , проходящая через точку
, проходящая через точку 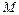 и целиком принадлежащая поверхности
и целиком принадлежащая поверхности 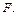 Обозначим
Обозначим  – точку пересечения прямой
– точку пересечения прямой 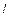 с направляющей. Так как по условию образующие параллельны вектору
с направляющей. Так как по условию образующие параллельны вектору 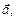 то
то 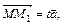 где
где  – некоторое действительное число, то есть,
– некоторое действительное число, то есть, 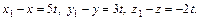 Откуда получим
Откуда получим 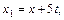
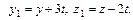 А так как точка
А так как точка 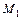 принадлежит направляющей, то
принадлежит направляющей, то 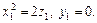 Исключив из уравнений параметр
Исключив из уравнений параметр  , получим уравнение цилиндрической поверхности
, получим уравнение цилиндрической поверхности
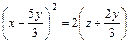
Вопросы для самоконтроля
1. Дать определение цилиндрической поверхности. Что называется направляющей и образующей цилиндрической поверхности? Можно ли назвать цилиндром: 1) прямую, 2) плоскость?
2. Как может быть задана аналитически поверхность?
3. Перечислить все виды цилиндрических поверхностей второго порядка и написать соответствующие им канонические уравнения.
4. Пусть Ф – поверхность, образованная всеми прямыми, каждая из которых проходит через некоторую точку линии 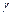 параллельно вектору
параллельно вектору  . Что можно сказать о поверхности Ф`, образованной всеми прямыми, каждая из которых проходит через некоторую точку линии
. Что можно сказать о поверхности Ф`, образованной всеми прямыми, каждая из которых проходит через некоторую точку линии 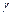 параллельно вектору –
параллельно вектору –  ?
?
5. Дать определение конической поверхности. Что называется вершиной и образующей конической поверхности? Можно ли назвать конусом: 1) прямую, 2) плоскость?
6. Существует ли поверхность, которая является одновременно и цилиндрической и конической?
7. Как записывается каноническое уравнение:
а) конической поверхности второго порядка; б) кругового конуса?
8. Что называется коническим сечением? Какими линиями могут быть:
а) конические сечения, б) сечения конуса второго порядка плоскостями, проходящими через его вершину?
9. Существуют ли поверхности второго порядка, обладающие тем свойством, что:
а) если некоторые точки А и В принадлежат этой поверхности, то прямая АВ целиком принадлежит поверхности,
б) вместе с любыми двумя своими точками А и В поверхность содержит все точки прямой АВ ?
10. Верно ли утверждение, что:
а) любое сечение поверхности второго порядка есть линия второго порядка, б) любую линию второго порядка можно рассматривать как сечение некоторой поверхности второго порядка?
11. Линии 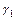 и
и 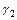 являются сечениями круговой конической поверхности Ф двумя параллельными плоскостями. Что можно сказать о линии
являются сечениями круговой конической поверхности Ф двумя параллельными плоскостями. Что можно сказать о линии 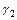 , если
, если 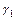 является:
является:
а) эллипсом, б) гиперболой, в) параболой?
12. Сколько прямых, лежащих на поверхности, можно провести через точку:
а) цилиндрической поверхности второго порядка,
б) конической поверхности второго порядка?
13. Приведите пример поверхности, которая: а) является поверхностью вращения, но не является ни цилиндром, ни конусом; б) является цилиндром, но не является ни поверхностью вращения, ни конусом; в) является конусом, но не является ни цилиндром, ни поверхностью вращения; г) является поверхностью вращения и цилиндром, но не является конусом; д) является одновременно и поверхностью вращения, и цилиндром, и конусом.
Задачи
1. Написать уравнение круговой цилиндрической поверхности, если известны её ось и точка А этой поверхности:
а) 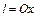 , А(1, 1, 1), б)
, А(1, 1, 1), б) 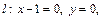 А(2, -
А(2, - 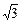 , 13).
, 13).
2. Написать уравнение цилиндрической поверхности, у которой:
а) направляющая лежит в плоскости 0xy и имеет уравнения:
x2 + 2xy + 3y2 – x = 0, z = 0, а образующие параллельны вектору  (1, 0, 1),
(1, 0, 1),
б) направляющая задана уравнениями
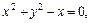
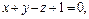
а образующие параллельны вектору  (1, –1, 2).
(1, –1, 2).
3. Написать уравнения прямолинейных образующих поверхности x2 + y2 = 4, проходящих через её точку А(0, 2, 3).
4. Написать уравнение конической поверхности, если известно, что её:
а) направляющая лежит в плоскости 0xy и задана в этой плоскости уравнением x2 + y2 – y = 0, а вершиной является точка S (1,0,1); б) направляющая задана уравнениями 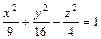 , x + y = 0, а вершиной является точка S(1,0,–1).
, x + y = 0, а вершиной является точка S(1,0,–1).
5. Написать уравнение круговой конической поверхности, если известны уравнения ее оси 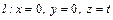 и координаты одной из ее точек
и координаты одной из ее точек 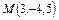 .
.
6. Написать уравнения прямолинейных образующих поверхности 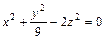 , параллельных плоскости 3x – y + 10 = 0.
, параллельных плоскости 3x – y + 10 = 0.
7. Найти проекцию на плоскость 0xy линии пересечения конуса, заданного уравнением 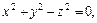 с плоскостью, имеющей уравнение
с плоскостью, имеющей уравнение 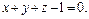
Домашнее задание
1. а) Написать уравнение круговой цилиндрической поверхности, если известны уравнения ее оси 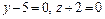 и точка
и точка 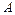 (18,5, –1), принадлежащая этой поверхности,
(18,5, –1), принадлежащая этой поверхности,
б) написать уравнение цилиндрической поверхности, если известно, что ее направляющей является гипербола 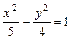 , z = 0, а образующие параллельны вектору
, z = 0, а образующие параллельны вектору 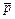 (1, 2, –1).
(1, 2, –1).
2. Написать уравнения прямолинейных образующих поверхности 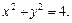 пересекающих прямую
пересекающих прямую 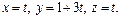
3. Написать уравнение:
а) круговой конической поверхности, вершиной которой является точка S(1,2,3), ось перпендикулярна к плоскости 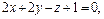 а образующие составляют с осью угол, равный 30°,
а образующие составляют с осью угол, равный 30°,
б) множества всех точек пространства, удаленных от данной прямой 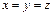 на расстояние, равное 2.
на расстояние, равное 2.
4. Написать уравнения прямолинейной образующей поверхности 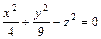 , проходящей через ее точку А(2,0,1).
, проходящей через ее точку А(2,0,1).
5. Найти первые две координаты точки В, если ее третья координата равна –13 и известно, что прямая АВ, где А(0,2,3) , всеми своими точками лежит на поверхности, заданной уравнением
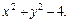
Задачи повышенной трудности
1. Написать уравнение цилиндрической поверхности вращения, если известны уравнения трех ее образующих 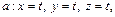
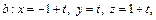
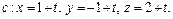
2. Найти множество всех точек, отношение расстояний от каждой из которых до двух пересекающихся прямых постоянно.
3. В пространстве даны три линии уравнениями:
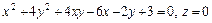 (парабола),
(парабола),
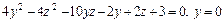 (гипербола),
(гипербола),
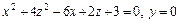 (эллипс).
(эллипс).
Доказать, что эти линии лежат на одной конической поверхности с вершиной (1, 1,1) и написать уравнение этой поверхности.
4. Найдите множество точек пространства, равноудаленных от двух данных параллельных прямых.
Тема 2.9. Эллипсоид. Гиперболоиды. Параболоиды
Литература: [1], гл. 18, § 4–6, стр. 482–504; [2], гл. 7, § 4–6,
стр. 201–218; [27], гл.9, §78-80, стр.271-283.
Основные определения, теоремы и формулы
Эллипсоидом называется поверхность, которая в некоторой прямоугольной системе координат определяется уравнением
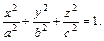
Однополостным гиперболоидом называется поверхность, которая в некоторой прямоугольной системе координат определяется уравнением
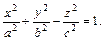
Его асимптотический конус имеет уравнение
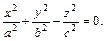
Двуполостным гиперболоидом называется поверхность, которая в некоторой прямоугольной системе координат определяется уравнением
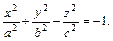
Эллиптическим параболоидом называется поверхность, которая в некоторой прямоугольной системе координат определяется уравнением
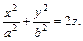
Гиперболическим параболоидом называется поверхность, которая в некоторой прямоугольной системе координат определяется уравнением
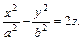
Прямая, лежащая на поверхности, называется прямолинейной образующей этой поверхности.
Пример. Найти прямолинейные образующие однополостного гиперболоида
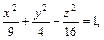
проходящие через его точку 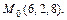
Решение. Уравнение однополостного гиперболоида можно представить в виде
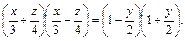
Значит, уравнения прямолинейных образующих имеют вид
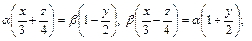
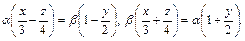
Подставив сюда значения 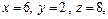 из первой системы получим
из первой системы получим 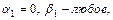 а из второй системы -
а из второй системы - 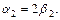 Значит, искомые прямолинейные образующие задаются уравнениями
Значит, искомые прямолинейные образующие задаются уравнениями
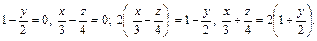
Вопросы для самоконтроля
1. Какая поверхность называется эллипсоидом? Что называется каноническим уравнением, полуосями, вершинами эллипсоида?
2. Эллипсоид задан в прямоугольной декартовой системе координат своим каноническим уравнением 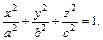 Верно ли утверждение, что его сечениями плоскостями, параллельными одной из координатных плоскостей, являются:
Верно ли утверждение, что его сечениями плоскостями, параллельными одной из координатных плоскостей, являются:
а) линии второго порядка одного типа, б) аффинно-эквивалентные линии, в) подобные линии второго порядка?
3. Как записывается каноническое уравнение эллипсоида, для которого:
а) ось 0x (0y) является осью вращения, б) обе оси 0x и 0y являются осями вращения?
4. Как доказать, что:
а) любой эллипсоид аффинно-эквивалентен сфере, б) любые два эллипсоида аффинно-эквивалентны?
5. Что представляют собой сечения эллипсоида различными плоскостями?
6. Существует ли в пространстве прямая:
а) которая не имеет общих точек с данным эллипсоидом, б) все точки, которой принадлежат данному эллипсоиду?
7. Какая поверхность называется однополостным гиперболоидом? Что называется каноническим уравнением, полуосями, вершинами, действительными и мнимой осями однополостного гиперболоида?
8. Как записывается каноническое уравнение однополостного гиперболоида, для которого ось 0x (0y) является осью вращения?
9. Что называется однополостным гиперболоидом вращения? Каким образом любой однополостной гиперболоид может быть получен из однополостного гиперболоида вращения?
10. Верно ли утверждение, что любые два однополостных гиперболоида аффинно-эквивалентны?
11. Что называется асимптотическим конусом однополостного гиперболоида?
12. Что представляют собой сечения однополостного гиперболоида плоскостями, проходящими через его мнимую ось? Каким может быть пересечение этой поверхности с прямыми, лежащими в таких плоскостях?
13. Существует ли в пространстве прямая:
а) которая не имеет общих точек с данным однополостным гиперболоидом,
б) все точки, которой принадлежат этой поверхности?
14. Какая поверхность называется двуполостным гиперболоидом. Что называется каноническим уравнением, полуосями, вершинами, вещественной и мнимыми осями двуполостного гиперболоида?
15. Ответить для двуполостного гиперболоида на вопросы, аналогичные вопросам 8–13, сформулированным для однополостного гиперболоида.
16. Какая поверхность называется эллиптическим параболоидом. Что называется каноническим уравнением, осью, вершиной эллиптического параболоида?
17. Ответить для эллиптического параболоида на вопрос 2, сформулированный для эллипсоида.
18. Что называется параболоидом вращения? Каким образом любой эллиптический параболоид может быть получен из параболоида вращения?
19. Верно ли утверждение, что любые два эллиптических параболоида аффинно-эквивалентны?
20. Что представляют собой сечения эллиптического параболоида плоскостями, проходящими через его ось или параллельными ей? Каким может быть пересечение поверхности с прямыми, лежащими в таких плоскостях?
21. Существует ли в пространстве прямая, все точки которой принадлежат данному эллиптическому параболоиду?
22. Какая поверхность называется гиперболическим параболоидом? Что называется каноническим уравнением, осью, вершиной гиперболического параболоида?
23. Ответить для гиперболического параболоида на вопрос 2, сформулированный для эллипсоида.
24. Как можно, используя две параболы (подвижную и неподвижную), получить гиперболический параболоид?
25. Верно ли утверждение, что любые два гиперболических параболоида аффинно-эквивалентны?
26. Существует ли в пространстве прямая:
а) которая на имеет общих точек с данным гиперболическим параболоидом,
б) все точки, которой принадлежат поверхности?
27. Что называется прямолинейной образующей поверхности?
28. Привести примеры поверхностей второго порядка, которые:
а) имеют прямолинейные образующие,
б) не имеют прямолинейных образующих.
29. Написать уравнение прямой, которая проходит через данную точку: а) однополостного гиперболоида, б) гиперболического параболоида, заданного каноническим уравнением.
30. Как написать параметрические уравнения прямолинейной образующей, проходящей через данную точку  поверхности второго порядка, которая задана своим уравнением
поверхности второго порядка, которая задана своим уравнением
F(x, y, z) = 0 в аффинной системе координат?
Задачи
1. Написать каноническое уравнение эллипсоида, который:
а) проходит через точку (2,0,1) и содержит эллипс, данный уравнениями 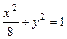 ,
, 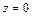 , б) пересекает плоскость 0yz по эллипсу
, б) пересекает плоскость 0yz по эллипсу 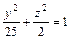 , а плоскость 0xy – по окружности x2 + y2 = 25.
, а плоскость 0xy – по окружности x2 + y2 = 25.
2. Найти множество всех точек пространства, расстояние от каждой из которых до точки (4,0,0) вдвое больше расстояния до плоскости, заданной уравнением х – 1 = 0.
3. Даны плоскость и точка А вне этой плоскости. Доказать, что множество всех точек, одинаково удалённых от данной плоскости и данной точки А, является параболоидом вращения.
4. Даны две параболы своими уравнениями y2 = 2x, 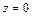 и
и 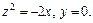 Написать уравнение поверхности, образованной прямой, которая пересекает эти параболы, оставаясь параллельной плоскости
Написать уравнение поверхности, образованной прямой, которая пересекает эти параболы, оставаясь параллельной плоскости 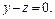
5. Напишите каноническое уравнение гиперболического параболоида с вершиной в начале координат, ось которого совпадает с осью Oy, если известно, что он проходит через точки A(1,1,6) и B(0, –1,1/5)
6. Написать уравнения прямолинейных образующих гиперболического параболоида, заданного уравнением 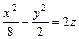 ;
;
а) проходящих через начало координат, б) параллельных плоскости, имеющей уравнение 6x + 4y – 8z + 1 = 0.
7. Написать уравнения прямых, проходящих через начало координат и целиком лежащих на поверхности, заданной уравнением
z = xy в аффинной системе координат.
8. Докажите, что через две пересекающиеся прямые в пространстве проходит поверхность второго порядка. Единственная ли эта поверхность?
Домашнее задание
1. Найти множество всех точек пространства, сумма расстояний от каждой из которых до точек (–4,0,0) и (4,0,0) равна 10.
2. Даны плоскость 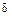 и точка А, не лежащая в этой плоскости, а также действительное число n, большее единицы. Доказать, что множество всех, для каждой из которых расстояние от точки А в n раз больше расстояния до плоскости
и точка А, не лежащая в этой плоскости, а также действительное число n, большее единицы. Доказать, что множество всех, для каждой из которых расстояние от точки А в n раз больше расстояния до плоскости 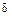 , является двуполостным гиперболоидом вращения.
, является двуполостным гиперболоидом вращения.
3. Написать каноническое уравнение:
а) эллиптического параболоида, проходящего через точки
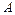 (1,0,1) и
(1,0,1) и  (0,2,1),
(0,2,1),
б) гиперболического параболоида, проходящего через точки (1,0,1) и (0,12,–1).
4. Написать уравнения прямых, проходящих через точку (6,2,8) и имеющих с поверхностью, заданной уравнением 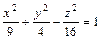 , более двух общих точек.
, более двух общих точек.
Задачи повышенной трудности
1. Найти множество всех точек пространства, для каждой из которых отношение расстояний до двух скрещивающихся перпендикулярных прямых равно данному положительному действительному числу 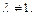
2. Даны две скрещивающиеся прямые  и
и  Что представляет поверхность, образованная вращением прямой
Что представляет поверхность, образованная вращением прямой  вокруг прямой
вокруг прямой 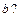
3. Найти множество всех точек пространства, каждая из которых равноудалена от двух скрещивающихся прямых.
4. Доказать, что гиперболический параболоид нельзя пересечь плоскостью по эллипсу.
Тема 2.10. Изображение тел, ограниченных поверхностями