Взаимное расположение плоскостей
Литература: [1], гл.10, §1, 3, стр. 230–238; [3], гл 2, §2, стр. 46–54; [27], гл.7, §59-61, стр. 211-220.
Основные определения, теоремы и формулы
Уравнение плоскости, заданной точкой  и некол- линеарными векторами
и некол- линеарными векторами  имеет вид
имеет вид
 или
или 
Последние уравнения называются параметрическими уравнениями.
Уравнение плоскости всегда можно привести к следующему виду:
 где
где 
которое называется общим уравнением плоскости.
Лемма. Вектор  параллелен плоскости
параллелен плоскости  , заданной общим уравнением
, заданной общим уравнением  тогда и только тогда, когда выполняется равенство
тогда и только тогда, когда выполняется равенство 
Пусть в аффинной системе координат даны две плоскости  и
и  своими уравнениями:
своими уравнениями:


Обозначим  ,
,  .
.
Плоскости  и
и  совпадают тогда и только тогда, когда
совпадают тогда и только тогда, когда 
Плоскости  и
и  параллельны, но различны тогда и только тогда, когда
параллельны, но различны тогда и только тогда, когда 
Плоскости  и
и  пересекаются по прямой тогда и только тогда, когда
пересекаются по прямой тогда и только тогда, когда 
Пример 1. Составить уравнение плоскости, проходящей через:
1) точку  параллельно плоскости
параллельно плоскости  2) точку
2) точку  и ось
и ось  две точки
две точки  и
и  параллельно оси
параллельно оси 
Решение. 1) Так как искомая плоскость  параллельна плоскости
параллельна плоскости  то векторы
то векторы  и
и  – направляющие векторы осей
– направляющие векторы осей  и
и  параллельны ей. Поэтому плоскость
параллельны ей. Поэтому плоскость  задается точкой
задается точкой  и векторами
и векторами  и
и  :
:
 или
или 
2) Выберем на оси  две точки, например,
две точки, например,  и
и  . Так как ось
. Так как ось  принадлежит плоскости
принадлежит плоскости  , то и точки
, то и точки  принадлежат
принадлежат  . Значит, плоскость
. Значит, плоскость  определяется тремя точками
определяется тремя точками  или точкой
или точкой 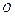 и двумя векторами
и двумя векторами  и
и  Ее уравнение примет вид
Ее уравнение примет вид
 или
или 
Пример 2. Составить параметрические уравнения плоскости

Решение. 1-й способ. Любые две из трех переменных 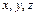 можно принять за независимые параметры. Положив, например,
можно принять за независимые параметры. Положив, например,  из уравнения плоскости найдем
из уравнения плоскости найдем  Искомые параметрические уравнения можно записать следующим образом:
Искомые параметрические уравнения можно записать следующим образом: 

2-й способ. Как известно, если плоскость задана общим уравнением  то векторы
то векторы

принадлежат направляющему подпространству этой плоскости, и какие-либо два из них образуют базис этого пространства. Значит, векторы  параллельны данной плоскости. Замечаем, что точка
параллельны данной плоскости. Замечаем, что точка  принадлежит плоскости. Следовательно, плоскость можно задать точкой
принадлежит плоскости. Следовательно, плоскость можно задать точкой  и векторами
и векторами 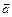 и
и 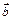 :
:

Вопросы для самоконтроля
1. Что называется направляющим подпространством плоскости?
2. Как записывается в векторном виде уравнение плоскости, заданной:
а) точкой  и базисом
и базисом  направляющего подпространства L,
направляющего подпространства L,
б) тремя точками М1, М2, М3, не лежащими на одной прямой,
в) точкой  и прямой m, лежащими в этой плоскости
и прямой m, лежащими в этой плоскости 
г) двумя пересекающимися прямыми а и b,
д) двумя параллельными прямыми а и b,
е) точкой  и перпендикулярным вектором
и перпендикулярным вектором  ?
?
Предполагается, что в случаях в), г), д) прямые заданы точкой и направляющим вектором.
3. Как запишется уравнение плоскости в каждом из случаев а) – д) (см. вопрос 2), если в пространстве задана аффинная система координат О  ? Какой вид имеет уравнение плоскости в случае е (см. вопрос 2), если в пространстве задана прямоугольная декартова система координат?
? Какой вид имеет уравнение плоскости в случае е (см. вопрос 2), если в пространстве задана прямоугольная декартова система координат?
4. Какой вид имеют векторное параметрическое уравнение и параметрические уравнения плоскости, заданной точкой  и базисом
и базисом 
 направляющего подпространства?
направляющего подпространства?
5. Написать векторное и параметрические уравнения для каждой из координатных плоскостей системы координат О  .
.
6. Что определяет в аффинной системе координат уравнение вида:
а)  где A, B, C, D – вещественные числа,
где A, B, C, D – вещественные числа,
б)  где A, B, C, D – вещественные числа и
где A, B, C, D – вещественные числа и
A2 + B2+C2> 0?
7. Какое уравнение называется общим уравнением плоскости?
8. Как из параметрических уравнений плоскости получить её общее уравнение? Как решается обратная задача?
9. Как сформулировать критерий параллельности вектора  (p1, p2, p3) и плоскости, заданной уравнением
(p1, p2, p3) и плоскости, заданной уравнением  ?
?
10. Как расположен вектор  (А, В, С) по отношению к плоскости, имеющей уравнение
(А, В, С) по отношению к плоскости, имеющей уравнение  если система координат: а) аффинная, б) прямоугольная декартова? –
если система координат: а) аффинная, б) прямоугольная декартова? –
11. Плоскость в аффинной системе координат задана общим уравнением  Как расположена плоскость по отношению к системе координат, если:
Как расположена плоскость по отношению к системе координат, если:
а)  б)
б)  в)
в)  г)
г)  д)
д) 
12. Что определяется в аффинной системе координат каждым из следующих условий:
а)  б)
б) 
в) 
Здесь А, В, С, D – вещественные числа и А2 + В2 + С2> 0.
13. Как выяснить, имеет ли плоскость, заданная общим уравнением  пересечение с внутренностью тетраэдра ABCD, где А(а1, а2, а3), В(b1, b2, b3), C(c1, c2, c3), D(d1, d2, d3)?
пересечение с внутренностью тетраэдра ABCD, где А(а1, а2, а3), В(b1, b2, b3), C(c1, c2, c3), D(d1, d2, d3)?
14. Как выяснить взаимное расположение двух плоскостей, заданных своими общими уравнениями А1x + B1y + C1z + D1 = 0и
А2x + B2y + C2z + D2 =0?
15. Какой вид имеет уравнение произвольной плоскости:
а) параллельной плоскости 
б) проходящей через фиксированную точку 
в) параллельной данному вектору 
Задачи
1. Написать уравнение плоскости, которая:
а) параллельна координатной плоскости 0xz и проходит через точку А(2, –5,3),
б) содержит ось аппликат и точку В(–3, 1, –2),
в) параллельна оси абсцисс и проходит через точки С(4, 0, –2) и
D (5, 1, 7).
2. Написать параметрические уравнения плоскости, которая проходит через точку А(2, –1, 3) параллельно плоскости, заданной уравнением  Перейти от полученных параметрических уравнений к общему уравнению плоскости. В какой системе координат решается задача?
Перейти от полученных параметрических уравнений к общему уравнению плоскости. В какой системе координат решается задача?
3. В аффинной системе координат две плоскости заданы уравнениями  и
и  Записать систему неравенств, определяющую тот двугранный угол, образованный этими плоскостями, которому принадлежит:
Записать систему неравенств, определяющую тот двугранный угол, образованный этими плоскостями, которому принадлежит:
а) начало координат, б) точка А(3, –4, 3).
4. При каких значениях параметров  и
и  плоскости, заданные в аффинной системе координат уравнениями
плоскости, заданные в аффинной системе координат уравнениями  и
и 
а) параллельны, б) совпадают, в) пересекаются?
5. Через точку А(–5, 16, 12) проведены две плоскости, одна из которых содержит ось абсцисс, вторая – ось ординат. Найти косинус угла между этими плоскостями.
6. Написать уравнение плоскости, проходящей через начало координат и перпендикулярной к линии пересечения плоскостей, заданных уравнениями  и
и 
Домашнее задание
1. Написать параметрические уравнения плоскости, заданной в аффинной системе координат общим уравнением:
а) 
б) 
2. Найти координаты точки, принадлежащей плоскости, и координаты двух векторов, образующих базис направляющего подпространства этой плоскости.
3. Написать общее уравнение плоскости, заданной в аффинной системе координат параметрическими уравнениями:
а) 
б) 
4. Найти основание перпендикуляра, проведенного из точки Р(1, 3, 5) к прямой, по которой пересекаются плоскости  и
и 
5. Даны две точки А(1, 3, –2) и В(7, –4, 4). Через точку В проведена плоскость, перпендикулярная прямой АВ. Написать ее уравнение.
6. Найти множество всех точек пространства, каждая из которых равноудалена от точек А(2, –1, 3) и В(4, 5, –3).
Задачи повышенной трудности
1. Плоскость  вместе с координатными плоскостями образует некоторый тетраэдр. Найти ребро куба, который можно поместить внутрь этого тетраэдра так, чтобы три грани его лежали на координатных плоскостях, а вершина, противоположная началу координат, лежала в данной плоскости.
вместе с координатными плоскостями образует некоторый тетраэдр. Найти ребро куба, который можно поместить внутрь этого тетраэдра так, чтобы три грани его лежали на координатных плоскостях, а вершина, противоположная началу координат, лежала в данной плоскости.
2. Написать уравнение плоскости, перпендикулярной плоскости  и пересекающей ее по прямой, лежащей в координатной плоскости
и пересекающей ее по прямой, лежащей в координатной плоскости 
Тема 5.6. Уравнения прямой. Взаимное расположение двух прямых, прямой и плоскости в пространстве. Метрические задачи теории прямых и плоскостей
Литература: [1], гл.10, §4, 6, 8-10, стр. 241–244, 246-247, 249-259; [3], гл. 2, §2–3, стр. 46–65; [27], гл.7, § 64-66, стр. 226-234.
Основные определения, теоремы и формулы
Положение прямой в пространстве определяется полностью, если даны: а) направляющий вектор прямой и некоторая ее точка; б) две точки прямой; в) две плоскости, пересекающиеся по этой прямой.
В аффинной системе координат уравнению прямой, заданной точкой  и направляющим вектором
и направляющим вектором  , можно придать один из следующих видов:
, можно придать один из следующих видов:
а)  . Эти уравнения называются параметрическими уравнениями прямой, а
. Эти уравнения называются параметрическими уравнениями прямой, а  – параметром;
– параметром;
б) если ни одна из координат вектора  неравна нулю
неравна нулю

если одна из координат вектора  равна нулю, например,
равна нулю, например,
 то
то 
если равны нулю две координаты вектора  , например,
, например,
 то
то 
Лемма. Если в аффинной системе координат прямая задана как пересечение двух плоскостей уравнениями  ,
,  , то вектор
, то вектор

является направляющим вектором этой прямой.
Вопросы для самоконтроля
1. Дать определение направляющего вектора прямой. Верно ли, что все направляющие векторы данной прямой образуют одномерное векторное подпространство?
2. Перечислить основные способы задания прямой. Какой вид имеет векторное параметрическое уравнение прямой?
3. Как записываются в аффинной системе координат:
а) параметрические уравнения прямой,
б) канонические уравнения прямой, если прямая задана точкой  и направляющим вектором
и направляющим вектором  или двумя своими точками
или двумя своими точками  и
и 
4. Какая фигура задаётся в аффинной системе координат системой уравнений вида:
 (1)
(1)
где: а)  – произвольные вещественные числа (i = 1, 2);
– произвольные вещественные числа (i = 1, 2);
б)  и
и  ,
,
в)  ,
,  , и числа А1, В1, С1 не пропорциональны числам А2 В2 С2.
, и числа А1, В1, С1 не пропорциональны числам А2 В2 С2.
5. Как найти направляющий вектор прямой, заданной общими уравнениями (1) в аффинной системе координат?
6. Как связан вектор  с векторами
с векторами  (А1, В1, С1) и
(А1, В1, С1) и  (А2, В2, С2), перпендикулярными пересекающимся плоскостям, которые заданы уравнениями системы (1), в случае, когда система координат прямоугольная декартова?
(А2, В2, С2), перпендикулярными пересекающимся плоскостям, которые заданы уравнениями системы (1), в случае, когда система координат прямоугольная декартова?
7. Прямая задана в аффинной системе координат системой уравнений (1). Каким условиям удовлетворяют коэффициенты системы (1), если эта прямая:
а) лежит в координатной плоскости 0xy,
б) параллельна оси аппарата,
в) совпадает с осью абсцисс,
г) проходит через начало координат?
8. Что можно сказать о взаимном расположении прямых а и b, заданных соответственно точкой А и направляющим вектором 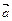 , точкой В и направляющим вектор
, точкой В и направляющим вектор  , если:
, если:
а) (  ) № 0, б) (
) № 0, б) (  ) = 0, в)
) = 0, в)  и (
и (  ) № 0,
) № 0,
г)  ,
,  (
(  ) = 0,
) = 0,
д)  =
=  =
=  , (
, (  ) = 0?
) = 0?
9. Прямая d задана точкой А и направляющим векторов  , плоскость
, плоскость  – точкой В и базисом
– точкой В и базисом  направляющего подпространства. Что можно сказать о взаимном расположении прямой d и плоскости
направляющего подпространства. Что можно сказать о взаимном расположении прямой d и плоскости  , если известно, что:
, если известно, что:
а)  б)
б)  и А
и А 
 , в)
, в)  и
и  ?
?
10. Что называется углом между:
а) двумя прямыми, б) прямой и плоскостью, в) двумя плоскостями? Как вычислить этот угол?
11. Доказать, что если а и b – скрещивающиеся прямые с направляющими векторами  , то две плоскости, проходящие соответственно через прямые а и b, параллельные вектору
, то две плоскости, проходящие соответственно через прямые а и b, параллельные вектору  , пересекаются по прямой, которая пересекает каждую из прямых а и b и перпендикулярна к этим прямым.
, пересекаются по прямой, которая пересекает каждую из прямых а и b и перпендикулярна к этим прямым.
12. В пространстве даны точка М и плоскость  , заданная точкой С и базисом
, заданная точкой С и базисом  направляющего подпространства. Определить, по какой из следующих формул можно найти расстояние
направляющего подпространства. Определить, по какой из следующих формул можно найти расстояние  от точки М до плоскости
от точки М до плоскости  :
:
а)  , б)
, б)  , в)
, в) 
13. Написать формулу, по которой вычисляется расстояние от точки  до плоскости, заданной уравнением
до плоскости, заданной уравнением  .
.
14. Две параллельные плоскости заданы уравнениями  и
и  Доказать, что расстояние
Доказать, что расстояние  между ними может быть найдено по формуле:
между ними может быть найдено по формуле:
 .
.
15. В пространстве через точки А и В проведены две прямые а и b с общим направляющим вектором  . Определить, по какой из формул можно найти расстояние
. Определить, по какой из формул можно найти расстояние  между ними:
между ними:
а)  , б)
, б)  , в)
, в)  г)
г)  .
.
16. В пространстве даны две скрещивающиеся прямые а и b с направляющими векторами  , проходящие соответственно через точки А и В. Что называется расстоянием между этими прямыми? Определить, по какой из формул можно найти это расстояние:
, проходящие соответственно через точки А и В. Что называется расстоянием между этими прямыми? Определить, по какой из формул можно найти это расстояние:
а)  =
=  , б)
, б)  = АВ, в)
= АВ, в)  =
=  ,
,
г)  =
=  , д)
, д)  =
=  ?
?
17. Доказать, что  равно расстоянию от произвольной точки на прямой а до плоскости, которая параллельна этой прямой и проходит через прямую b.
равно расстоянию от произвольной точки на прямой а до плоскости, которая параллельна этой прямой и проходит через прямую b.
Пример 1.Составить уравнение плоскости  делящей пополам тот двугранный угол между плоскостями
делящей пополам тот двугранный угол между плоскостями
 и
и 
в котором лежит начало координат.
Решение. Способ 1. Плоскость  состоит из точек, равноудаленных от плоскостей
состоит из точек, равноудаленных от плоскостей  и
и  , то есть,
, то есть,  Считая координаты точки
Считая координаты точки 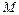 произвольными, получим:
произвольными, получим:

Значит, либо

либо 
Введем обозначения:



Так как  то для точек рассматриваемого двугранного угла имеем
то для точек рассматриваемого двугранного угла имеем  Следовательно, искомая плоскость
Следовательно, искомая плоскость
 или
или 
Задачи
1. Написать уравнения прямой:
а) проходящей через точку А(2,1,–3) и параллельной вектору  (1,–3,1);
(1,–3,1);
б) проходящей через точки А(2,–3,1/2) и В(3,5,3/2);
в) образованной пересечением плоскости x + 3y – z + 1 = 0 с плоскостью 0xy;
г) проходящей через точку А(1,–3,4) параллельно прямой, заданной системой уравнений 
д) проходящей через точку А (0,0,2) и перпендикулярной прямым, заданным уравнениям:

В случаях а) – г) система координат аффинная, в случае д) –прямоугольная декартова.
2. Определить взаимное расположение двух прямых, заданных в аффинной системе координат уравнениями:
а)  и
и  , б)
, б)  и
и 
в)  и
и 
3. Написать уравнения прямой, проходящей через точку А (2,3,1) и пересекающей прямые, заданные в аффинной системе координат уравнениями:
 и
и 
4. Найти уравнения ортогональной проекции прямой d заданной системой уравнений  , на координатную плоскость 0xy и величину угла, который прямая d образует с этой плоскостью.
, на координатную плоскость 0xy и величину угла, который прямая d образует с этой плоскостью.
5. Написать уравнения прямой, которая проходит через точку Р(2, –1, 0) и пересекает под прямым углом прямую, заданную уравнениями:

6. Найти точку, симметричную точке М(2,7,1) относительно плоскости, заданной уравнением  .
.
7. Написать уравнения прямой, содержащей общий перпендикуляр оси ординат и прямой, заданной уравнениями: 
8. Найти расстояние между прямыми
 и
и  :
:  .
.
9. На оси аппликат найти точку, которая удалена от плоскости  на расстояние
на расстояние  = 4.
= 4.
10. Даны плоскости  и
и  Найти угол между этими плоскостями и написать уравнение биссекторной плоскости того угла между ними, в котором лежит начало координат.
Найти угол между этими плоскостями и написать уравнение биссекторной плоскости того угла между ними, в котором лежит начало координат.
Домашнее задание
1. Доказать, что прямые, заданные уравнениями:
 и
и 
параллельны и написать уравнение прямой, относительно которой эти прямые симметричны.
2. Написать уравнения прямой, которая проходит через точку пересечения прямой  с плоскостью
с плоскостью  перпендикулярно к этой плоскости.
перпендикулярно к этой плоскости.
3. Написать уравнения проекции прямой, заданной в аффинной системе координат уравнениями  на плоскость
на плоскость
 если направление проектирования задано вектором
если направление проектирования задано вектором  (1,2,0).
(1,2,0).
4. Через точку пересечения оси абсцисс и плоскости, заданной в аффинной системе координат уравнением  проведена прямая так, что она лежит в этой плоскости и параллельна плоскости Оyz. Написать уравнения этой прямой.
проведена прямая так, что она лежит в этой плоскости и параллельна плоскости Оyz. Написать уравнения этой прямой.
5. Найти точку, симметричную точке А(4,3,10) относительно прямой, заданной уравнениями 
Задачи повышенной трудности
1. Даны три плоскости  имеющие одну общую точку. Найти расстояние от этой точки до плоскости
имеющие одну общую точку. Найти расстояние от этой точки до плоскости 
2. К сфере проведены две скрещивающиеся касательные  и
и  Найти множество точек касания касательных к сфере, пересекающих прямые
Найти множество точек касания касательных к сфере, пересекающих прямые  и
и 
3. Дан параллелепипед  . Доказать, что всякая прямая, пересекающая три из прямых
. Доказать, что всякая прямая, пересекающая три из прямых  пересекает и четвертую прямую или параллельна ей.
пересекает и четвертую прямую или параллельна ей.
Индивидуальные задания по теме
«Прямые и плоскости в пространстве»
Вариант 1.
1. Из одной точки отложены направленные отрезки - представители некомпланарных векторов  ,
,  . Доказать, что плоскость, проходящая через концы этих отрезков, перпендикулярна вектору
. Доказать, что плоскость, проходящая через концы этих отрезков, перпендикулярна вектору 
2. Дан тетраэдр, вершины которого находятся в точках 


 Найти: а) объем тетраэдра; б) площади граней; в) длину и уравнение высоты
Найти: а) объем тетраэдра; б) площади граней; в) длину и уравнение высоты  ; г) угол между ребрами
; г) угол между ребрами  и
и  ; д) уравнения граней
; д) уравнения граней  и
и  и угол между этими гранями.
и угол между этими гранями.
3. Написать уравнения прямой, пересекающей каждую из трёх прямых, заданных в аффинной системе координат уравнениями

 ,
, 
 ,
, 

4. Через линию пересечения плоскостей, заданных уравнениями  и
и  , провести плоскость, образующую угол p/4 с плоскостью, заданной уравнением
, провести плоскость, образующую угол p/4 с плоскостью, заданной уравнением 
5. Найти расстояние между прямыми, заданными уравнениями
 и
и 
и написать уравнения прямой, содержащей общий перпендикуляр этих прямых.
6. Доказать, что отрезки, соединяющие противоположные ребра тетраэдра, пересекаются в одной точке и делятся в ней пополам.
Вариант 2.
1. Дан тетраэдр, вершины которого находятся в точках  ,
, 

 Найти: а) объем тетраэдра; б) площади граней; в) длину и уравнение высоты
Найти: а) объем тетраэдра; б) площади граней; в) длину и уравнение высоты  ;
;
г) угол между ребрами  и
и  ; д) уравнения граней
; д) уравнения граней  и
и  и угол между этими гранями.
и угол между этими гранями.
2. Найти расстояние от точки  до прямой, проходящей через точки А(1,2,– 3) и В(5,2,0).
до прямой, проходящей через точки А(1,2,– 3) и В(5,2,0).
3. Написать уравнение плоскости, параллельной плоскости, заданной уравнением  и удалённой от неё на расстояние, равное 3.
и удалённой от неё на расстояние, равное 3.
4. Написать уравнения прямой, проходящей через точку  которая пересекает прямые, заданные в аффинной системе координат уравнениями
которая пересекает прямые, заданные в аффинной системе координат уравнениями
 и
и 
5. Написать уравнение плоскости, симметричной координатной плоскости 0xz относительно плоскости, заданной уравнением 
6. Пусть ребра AB, AC, AD тетраэдра ABCD взаимно перпендикулярны. Доказать, что центр сферы, описанной вокруг данного тетраэдра, лежит на прямой, соединяющей вершину A с центром тяжести треугольника BCD.
Вариант 3.
1. Найти объём шара, вписанного в тетраэдр, ограниченный координатными плоскостями и плоскостью, заданной уравнением

2. Написать уравнение плоскости, проходящей через начало координат и перпендикулярной к прямой, заданной уравнениями:
 .
.
3. Дан тетраэдр, вершины которого находятся в точках  B(5,–1,2), C(3,0,–3), D(6,1,–1). Найти: а) объем тетраэдра; б) площади граней; в) длину и уравнение высоты АН;
B(5,–1,2), C(3,0,–3), D(6,1,–1). Найти: а) объем тетраэдра; б) площади граней; в) длину и уравнение высоты АН;
г) угол между ребрами AB и CD; д) уравнения граней ABC и ABD и угол между этими гранями.
4. Написать уравнение плоскости g, которая параллельна плоскостям a и b, заданным соответственно уравнениями  и
и  если известно отношение расстояний
если известно отношение расстояний

5. Найти координаты точки, симметричной точке А(0,0,2) относительно прямой, заданной каноническими уравнениями
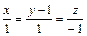 .
.
6. Доказать, что плоскости, перпендикулярные к ребрам тетраэдра и делящие их пополам, пересекаются в одной точке.
Вариант 4.
1. Найти площадь треугольника АВС, если  где
где 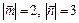 ,
,  .
.
2. Написать уравнение плоскости, проходящей через начало координат и перпендикулярной к двум плоскостям, заданным уравнениями  и
и 
3. Дан тетраэдр, вершины которого находятся в точках A(2, –1,1), B(5,–1,2), C(–3,0,–3), D(6,0,–1). Найти: а) объем тетраэдра; б) площади граней; в) длину и уравнение высоты АН; г) угол между ребрами AB и CD; д) уравнения граней ABC и ABD и угол между этими гранями.
4. Написать уравнения прямой, содержащей перпендикуляр, проведённой из точки А(2, 3, 1) к прямой, заданной уравнениями 
5. Даны координаты вершин тетраэдра АВСD: А(0,0,2), В(3,0,5), С(1,1,0), D(4,1,2). Вычислить его объём и составить уравнение прямой, содержащей общий перпендикуляр прямых АС и BD.
6. В неплоском четырехугольнике отрезки, соединяющие середины двух противоположных сторон и середины диагоналей пересекаются и делятся точкой пересечения пополам.
Вариант 5.
1. При каком значении параметра a векторы 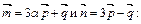
а) коллинеарны, б) перпендикулярны, если известно, что 
2. Дан тетраэдр, вершины которого находятся в точках A(2,1,–1), B(5,1,2), C(3,0,–3), D(6,0,–1). Найти: а) объем тетраэдра; б) площади граней; в) длину и уравнение высоты АН; г) угол между ребрами AB и CD; д) уравнения граней ABC и ABD и угол между этими гранями.
3. Написать уравнение плоскости, проходящей через начало координат и перпендикулярной к прямой, заданной уравнениями:
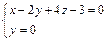
4. Найти расстояние между прямыми, заданными уравнениями
 и
и 
5. Написать уравнения прямой, проходящей через точку А(4,0,–1), которая пересекает прямые, заданные уравнениями
 и
и 
6. В неплоском четырехугольнике отрезки, соединяющие середины двух противоположных сторон и середины диагоналей пересекаются и делятся точкой пересечения пополам.
Вариант 6.
1. Вычислить площадь треугольника АВС, если известно, что  ,
, 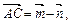 где
где  .
.
2. Дан тетраэдр, вершины которого находятся в точках
A(–2,–1,1), B(5,–1,–2), C(3,0,–3), D(6,0,–1). Найти: а) объем тетраэдра; б) площади граней; в) длину и уравнение высоты АН; г) угол между ребрами AB и CD; д) уравнения граней ABC и ABD и угол между этими гранями.
3. Написать уравнение множества всех точек пространства, равноудалённых от двух плоскостей, заданных уравнениями  и
и 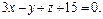
4. Найти величину угла между прямой, заданной уравнениями  и плоскостью, заданной уравнением
и плоскостью, заданной уравнением 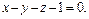
5. Написать уравнения прямой, проходящей через точку
М(2,–1,0), которая пересекает под прямым углом прямую, заданную уравнениями 
6. Доказать, что две плоскости, проведенные через вершины A1BD и CB1D1, делят диагональ AC1 параллелепипеда ABCDA1B1C1D1 на три равные части.
Вариант 7.
1. Дан тетраэдр, вершины которого находятся в точках A(2,–1,2), B(5,1,2), C(3,0,–3), D(6.0,–1). Найти: а) объем тетраэдра; б) площади граней; в) длину и уравнение высоты АН; г) угол между ребрами AB и CD; д) уравнения граней ABC и ABD и угол между этими гранями.
2. Дан куб ABCDA1B1C1D1, ребро которого равно 3. Найти расстояние от вершины А до плоскости BMN, где М и N – середины рёбер DC и D1C1соответственно.
3. Написать уравнения прямой, проходящей через точку
А(1,0,1) и перпендикулярной к плоскости, заданной уравнением 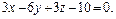 Найти расстояние между этой прямой и осью абсцисс.
Найти расстояние между этой прямой и осью абсцисс.
4. Выяснить взаимное расположение прямых, заданных в аффинной системе координат уравнениями
 и
и 
5. Найти расстояние между скрещивающимися прямыми, заданными уравнениями
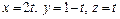 и
и 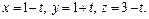
6. Доказать, что диагональ AC1параллелепипеда ABCDA1B1C1D1 проходит через центры тяжести треугольников A1BD и B1D1C.
Вариант 8.
1. При каком значении 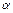 векторы
векторы 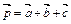 ,
,  ,
,  компланарны, если известно, что
компланарны, если известно, что 
2. В треугольной призме ABCA1B1C1векторы  (1,2,1),
(1,2,1),  (3,0,2) определяют основание, а вектор АА1(–1, 0, 0) – боковое ребро. Найти объём призмы и площадь грани АВВ1А1.
(3,0,2) определяют основание, а вектор АА1(–1, 0, 0) – боковое ребро. Найти объём призмы и площадь грани АВВ1А1.
3. Найти расстояние от точки С(3,2,–2) до прямой, проходящей через точки А(1, 2, –3) и В(5, 2, 0).
4. Дан тетраэдр, вершины которого находятся в точках A(0,0,0), B(3,4,–1), C(2,3,5), D(6,0,–3). Найти: а) объем параллелепипеда;
б) площади граней; в) длину и уравнение высоты АН; г) угол между ребрами AB и CD; д) уравнения граней ABC и ABD и угол между этими гранями.
5. Написать уравнения прямой, проходящей через точку  перпендикулярно прямым, заданным уравнениями:
перпендикулярно прямым, заданным уравнениями:
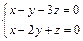 и
и 
6. В неплоском четырехугольнике отрезки, соединяющие середины двух противоположных сторон и середины диагоналей пересекаются и делятся точкой пересечения пополам.
Вариант 9.
1. Дан тетраэдр, вершины которого находятся в точках A(0,0,0), B(3,4,–1), C(2,3,5), D(6,0,–3). Найти: а) объем тетраэдра; б) площади граней; в) длину и уравнение высоты АН; г) угол между ребрами AB и CD; д) уравнения граней ABC и ABD и угол между этими гранями.
2. Написать уравнения прямой, которая проходит через точку А(1,2,–1) и параллельна прямой, заданной уравнениями:
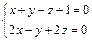 .
.
3. Выяснить взаимное расположение прямых, заданных в аффинной системе координат уравнениями:
 и
и 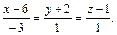
4. Написать уравнение плоскости, проходящей через линию пересечения плоскостей, заданных уравнениями  и
и  и перпендикулярной к плоскости, заданной уравнением
и перпендикулярной к плоскости, заданной уравнением 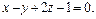
5. Написать уравнения прямой, содержащей общий перпендикуляр двух прямых, заданных уравнениями
 и
и  .
.
6. Докажите, что в неплоском четырехугольнике отрезки, соединяющие середины противоположных сторон пересекаются и делятся точкой пересечения пополам.
Вариант 10.
1. На оси абсцисс найти точку, равноудалённую от точки А(1,0,0) и плоскости, заданной уравнением 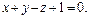
2. Выяснить взаимное расположение и вычислить угол между прямой  и плоскостью
и плоскостью 
3. Через точку 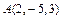 проведена прямая
проведена прямая  , параллельная прямой, заданной уравнениями
, параллельная прямой, заданной уравнениями  . Написать уравнения прямой, содержащей общий перпендикуляр прямой
. Написать уравнения прямой, содержащей общий перпендикуляр прямой  и оси аппликат.
и оси аппликат.
4. Найти точку, симметричную точке 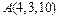 относительно прямой, заданной уравнениями
относительно прямой, заданной уравнениями 
5. Дан тетраэдр, вершины которого находятся в точках A(0,0,0), B(3,4,1), C(2,3,–5), D(6,0,–3). Найти: а) объем тетраэдра; б) площади граней; в) длину и уравнение высоты АН; г) угол между ребрами AB и CD; д) уравнения граней ABC и ABD и угол между этими гранями.
6. Пусть ребра AB, AC, AD тетраэдра ABCD взаимно перпендикулярны. Доказать, что центр сферы, описанной вокруг данного тетраэдра, лежит на прямой, соединяющей вершину A с центром тяжести треугольника BCD.
Вариант 11.
1. а) Найти координаты вектора  в ортонормированном базисе
в ортонормированном базисе  , если известно, что
, если известно, что  = 3, [
= 3, [  ] = – 2
] = – 2  .
.
2. Решить систему уравнений 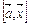 =
=  ,
,  =
=  , где
, где 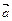 и
и  – данные векторы.
– данные векторы.
3. Дан тетраэдр, вершины которого находятся в точках A(0,0,0), B(3,4,–1), C(2,3,5), D(6,0,–3). Найти: а) объем тетраэдра; б) площади граней; в) длину и уравнение высоты АН; г) угол между ребрами AB и CD; д) уравнения граней ABC и ABD и угол между этими гранями.
4. Написать уравнения прямой, содержащей высоту АН треугольника АВС, если известны координаты его вершин А(4,1,2), В(3,0,5), С(1,1,0).
5. Написать уравнение плоскости, которая касается сферы  и проходит через прямую, заданную уравнениями
и проходит через прямую, заданную уравнениями

6. Найти расстояние между прямыми, заданными уравнениями:
 и
и 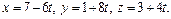
7. Из вершины произвольного параллелепипеда проведены три диагонали прилежащих граней. Установить, какую часть объема параллелепипеда составляет объем пирамиды, боковыми ребрами которой служат эти диагонали.
Вариант 12.
1. Дан тетраэдр, вершины которого находятся в точках A(0,0,0), B(3,4, –1), C(2,3,5), D(6,0, –3). Найти: а) объем тетраэдра; б) площади граней; в) длину и уравнение высоты АН; г) угол между ребрами AB и CD; д) уравнения граней ABC и ABD и угол между этими гранями.
2. Написать уравнение плоскости, которая проходит через начало координат и содержит перпендикуляр, проведённый из точки
А(1, –1,0) к прямой, заданной как пересечение двух плоскостей  и
и 
3. Найти координаты центров и радиусы сфер, каждая из которых касается координатных плоскостей и плоскости, заданной уравнением 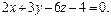
4. Написать уравнения прямой, которая проходит через точку А(3, –1, –4) параллельно плоскости, заданной в аффинной системе координат уравнением  и пересекает ось ординат.
и пересекает ось ординат.
5. Написать уравнение плоскости, которая касается сферы  и проходит через линию пересечения плоскостей, заданных уравнениями
и проходит через линию пересечения плоскостей, заданных уравнениями  и
и 
6. Вершины параллелепипеда и центры трех противоположных для данной вершины граней служат вершинами пирамиды. Установить, какую часть объема параллелепипеда составляет объем этой пирамиды.
Вариант 13.
1. К какой из осей координат ближе располагается прямая, заданная как линия пересечения двух плоскостей с уравнениями  и
и 
2. Дан тетраэдр, вершины которого находятся в точках A(0,1,0), B(3, –4, –1), C(2,3,5), D(6,0, –3). Найти: а) объем тетраэдра; б) площади граней; в) длину и уравнение высоты АН; г) угол между ребрами AB и CD; д) уравнения граней ABC и ABD и угол между этими гранями.
3. Написать уравнения прямой, которая симметрична прямой  относительно плоскости, заданной параметрическими уравнениями
относительно плоскости, заданной параметрическими уравнениями 
4. Написать уравнение плоскости, которая отстоит от точки
А(1,1, –2) на расстоянии, равном 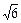 , и проходит через линию пересечения плоскостей, заданных уравнениями
, и проходит через линию пересечения плоскостей, заданных уравнениями  и
и  Какой угол составляет с этой плоскостью ось аппликат?
Какой угол составляет с этой плоскостью ось аппликат?
5. Найти координаты центра и радиус той из сфер, касающихся прямой  и одной из осей координат, радиус которой минимален.
и одной из осей координат, радиус которой минимален.
6. Дан тетраэдр АВСD и точка К на ребре АВ. Доказать, что середины отрезков АК, ВС, КD, и КС лежат в одной плоскости.
Вариант 14.
1. Дан тетраэдр, вершины которого находятся в точках A(0,0,0), B(3,4, –1), C(2,3,5), D(6,0, –3). Найти: а) объем тетраэдра; б) площади граней; в) длину и уравнение высоты АН; г) угол между ребрами AB и CD; д) уравнения граней ABC и ABD и угол между этими гранями.
2. Вычислить расстояние от точки А(0,1,1) до оси пучка плоскостей, заданного уравнением 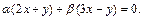
3. Написать уравнение той плоскости, касающейся сферы, заданной уравнением  которая проходит через ось аппликат.
которая проходит через ось аппликат.
4. Найти уравнения прямой  образующей равные углы с осями координат прямоугольной декартовой системы
образующей равные углы с осями координат прямоугольной декартовой системы 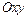 и написать уравнения ее ортогональной проекции на координатную плоскость
и написать уравнения ее ортогональной проекции на координатную плоскость 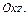
5. Написать параметрические уравнения прямой, содержащей общий перпендикуляр двух прямых, заданных уравнениями
 и
и 
6. Доказать, что во всяком неплоском четырехугольнике прямые, соединяющие середины смежных сторон, образуют параллелограмм.
Вариант 15.
1. Диагональ  прямоугольного параллелепипеда
прямоугольного параллелепипеда  образует углы по 600 с ребрами
образует углы по 600 с ребрами  и
и 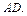 Какой угол она образует с ребром
Какой угол она образует с ребром 
2. Доказать, что начало координат находится внут