Формулы преобразования координат
Литература: [1], гл.3, §1,2, стр.55–62, гл.4, §1, стр.66–69, гл.8, §1,3, стр.188–193, 196-202; [2], ч.1, гл.3, §1–2, стр.89–96; [27], гл.6, §52-54, стр. 186-196.
Основные определения, теоремы и формулы
Четверка, состоящая из точки 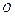 и базиса
и базиса  называется аффинной системой координат в пространстве и обозначается
называется аффинной системой координат в пространстве и обозначается 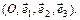 Точка
Точка 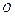 называется началом координат, а векторы
называется началом координат, а векторы 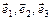 - координатными векторами.
- координатными векторами.
Координатами точки 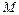 в системе
в системе 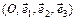 называются числа
называются числа 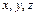 такие, что
такие, что 
Система координат называется прямоугольной декартовой или просто прямоугольной, если базис этой системы является ортонормированным. Такая система координат с началом в точке 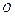 обозначается так:
обозначается так:  или
или  где
где 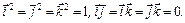
Замечание. Для решения аффинных задач в пространстве методом координат достаточно иметь аффинную систему координат. Метрические же задачи решаются в прямоугольной декартовой или просто декартовой системе координат. В дальнейшем, если не будет специальной оговорки, будем считать, что система координат соответствует типу решаемой задачи.
Вопросы для самоконтроля
1. Как, зная координаты точки, построить ее? Изобразите аффинную систему координат в пространстве и постройте точки с заданными координатами:

2. Как найти координаты точки в данной аффинной системе координат?
3. Известны координаты точек А и В в аффинной системе координат. Как найти координаты середины отрезка?
4. Что означает выражение “Точка М делит направленный отрезок  в отношении
в отношении 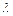 ”?
”?
5. В каком отношении делит направленный отрезок  :
:
а) точка 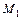 , б) точка М2, в) середина М отрезка
, б) точка М2, в) середина М отрезка  ?
?
6. Точка М делит направленный отрезок  в отношении
в отношении 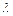 и направленный отрезок
и направленный отрезок 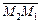 – в отношении
– в отношении  . Какова зависимость между
. Какова зависимость между 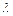 и
и  ? В каком случае
? В каком случае 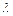 =
=  ?
?
7. Точка М делит направленный отрезок  в отношении
в отношении 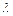 . Указать положение точки М относительно отрезка
. Указать положение точки М относительно отрезка  , если известно, что:
, если известно, что:
а) 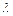 > 0, б) –1 <
> 0, б) –1 < 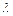 < 0, в)
< 0, в) 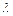 < –1, г)
< –1, г) 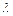 = 0 ?
= 0 ?
8. Как расположены точки М и N, делящие отрезок  соответственно в отношениях
соответственно в отношениях 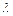 и
и 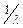 ?
?
9. Как перемещается по прямой М1М2 точка М (см. вопрос 7), если известно, что:
а) 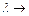 0, б)
0, б)  , в)
, в) 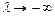 , г)
, г) 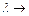 –1 ?
–1 ?
10. Как выражаются координаты точки М, делящей направленный отрезок  в отношении
в отношении 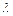 , через координаты точек М1, М2 и числом
, через координаты точек М1, М2 и числом 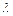 ?
?
11. Что называется прямоугольной декартовой системой координат в пространстве? Как вычислить длину отрезка М1М2, если его концы заданы своими координатами в прямоугольной декартовой системе координат: М1(x1, y1, z1), М2(x2, y2, z2)?
12. Какая система координат называется декартовой? Как решить задачу из предыдущего примера 11, если координаты точек определены в декартовой системе координат?
13. Как вводится понятие ориентации пространства? Какая система координат называется левой (правой)?
14. Система координат О  – правая. Какой будет система координат
– правая. Какой будет система координат 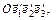 если:
если:
а) 
б) 
в) 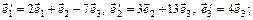
г) 
д) 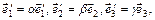 где
где  ;
;
е) 
ж) 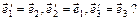
15. Являются ли одинаково ориентированными базисы 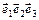 и
и  если: а)
если: а)  б)
б) 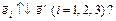
16. Какой вид имеют формулы преобразования аффинной системы координат в пространстве:
а) в общем случае, б) когда изменяется только начало координат, в) когда изменяются только базисные векторы?
17. Какой вид имеют формулы преобразования прямоугольной декартовой системы координат? Какие матрицы называются ортогональными? Является ли условие равенства ±1 определителя матрицы достаточным условием ее ортогональности?
18. Как по формулам преобразования координат определить, одинаково ли ориентированы старая и новая системы координат?
19. Могут ли одна (две, три, четыре) точки общего положения иметь одинаковые координаты в двух различных аффинных системах координат?
Задачи
1. Известны координаты четырёх вершин параллелепипеда ABCDA1B1C1D1: А (2,–1,1), В (1,3,4), D (6,0,1), А1 (4,2,0). Найти координаты остальных вершин и ориентацию базиса 
2. Даны точки А (2,–1,7), В (4,5,–2). Найти отношение, в котором каждая координатная плоскость делит отрезок  . Имеет ли прямая АВ точки пересечения с осями координат?
. Имеет ли прямая АВ точки пересечения с осями координат?
3. Написать формулы преобразования координат при переходе от аффинной системы координат О 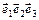 к системе О
к системе О  , если:
, если:
а)  (0, 3, –1),
(0, 3, –1), 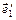 (1, 3, 0),
(1, 3, 0), 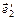 (0, –3, 1),
(0, –3, 1),  (1, 1, –2);
(1, 1, –2);
б)  (5, 0, –2),
(5, 0, –2), 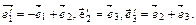
4. Дан тетраэдр ОАВС. Написать формулы преобразования координат точек при переходе от аффинной системы координат 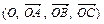 к системе
к системе 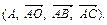
5. Какие из формул определяют преобразование координат точек при переходе от одной аффинной системы координат к другой:
а) 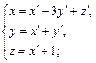 б)
б) 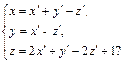
При положительном ответе найти координаты нового начала и новых координатных векторов соответственно в старой системе координат и её базисе.
67. Доказать, что четырёхугольник с вершинами в точках А (7,2,4), В (4,–4,2), С (6,–7,8), D (9,–1,10) является квадратом. В какой системе координат решается задача?
Домашнее задание
1. Найти координаты вершин тетраэдра АВСD в аффинной системе координат:
а)  ,
,
б) 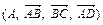 .
.
2.Найти координаты центра О параллелепипеда АВСDA1B1C1D1 и центра О1 его грани ВСС1В1 в аффинной системе координат:
а) 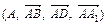 ,
,
б) 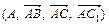 ,
,
в) 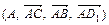 ,
,
г)  .
.
3. Отрезок АВ разделен на три равные части точками М1(1,2,3) и М2(3,4,3). Найти координаты точек А и В.
4. Ребро куба АВСDA1B1C1D1 равно 1. Найти зависимость между координатами произвольной точки М в системах координат:
а) 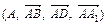 и
и 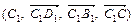 ;
;
б) 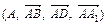 и
и 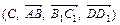 .
.
В каждом из случаев найти длину отрезка ВЕ, где Е – точка, имеющая одинаковые координаты в старой и новой системах координат.
5. Доказать, что четырехугольник с вершинами в точках А(7,8,9), В(9,3,7), С(5,4,3), D(3,9,5) является ромбом. Найти его площадь.
Задачи повышенной трудности
1. Доказать, что отрезки, соединяющие середины противоположных ребер тетраэдра пересекаются в одной точке и делятся в ней пополам.
2. В каком отношении плоскость, проходящая через концы трех ребер параллелепипеда, исходящих из одной вершины, делит его диагональ, выходящую из этой же вершины?
3. Доказать, что отрезки, соединяющие вершины тетраэдра с центрами тяжести противоположных граней, пересекаются в одной точке. Найти отношение, в котором эта точка делит построенные отрезки.
Тема5.2.Векторное произведение векторов
Литература: [1], гл. 9, § 4, стр. 225–230; [3], гл.1, § 4, стр. 29–30; [27], гл.6, §56, стр.200-204.
Основные определения, теоремы и формулы
Векторным произведением неколлинеарных векторов 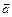 и
и 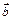 из ориентированного векторного пространства называется вектор, обозначаемый
из ориентированного векторного пространства называется вектор, обозначаемый  и удовлетворяющий следующим условиям:
и удовлетворяющий следующим условиям:
1) 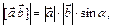 где
где 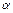 – направленный угол между векторами
– направленный угол между векторами 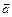 и
и 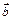 ,
,
2) вектор  перпендикулярен как вектору
перпендикулярен как вектору 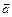 , так и вектору
, так и вектору 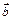 ,
,
3)  – правая тройка векторов.
– правая тройка векторов.
Из 2) и 3) видно, что вектор  направлен по правилу “правого винта” при вращении вектора
направлен по правилу “правого винта” при вращении вектора 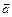 к вектору
к вектору 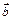 .
.
Векторное произведение коллинеарных векторов считается равным нуль-вектору.
Теорема 1. Если векторы 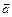 и
и 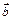 в правом ортонормированном базисе имеют координаты
в правом ортонормированном базисе имеют координаты 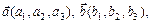 то вектор
то вектор

Теорема 2. Векторное произведение двух векторов 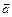 и
и 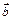 равно нуль-вектору тогда и только тогда, когда векторы
равно нуль-вектору тогда и только тогда, когда векторы 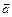 и
и 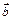 коллинеарны.
коллинеарны.
Теорема 3. Модуль векторного произведения двух векторов равен площади параллелограмма, построенного на векторах, как на сторонах.
Вопросы для самоконтроля
1. Сформулировать основные свойства векторного произведения векторов.
2. Как найти площадь треугольника ABC, если в прямоугольной декартовой системе координат вершины треугольника имеют координаты: А (а1, а2, а3), В (b1, b2, b3), С (с1, с2, с3)?
3. Векторы 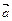 и
и  перпендикулярны вектору
перпендикулярны вектору 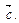 Что можно сказать о векторе [[
Что можно сказать о векторе [[ 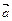
 ]
]  ]?
]?
4. Можно ли из условия [ 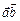 ] = [
] = [ 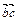 ], где
], где  , заключить, что
, заключить, что 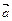 =
=  ?
?
5. Верно ли утверждение о том, что векторы 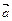 и
и  коллинеарны тогда и только тогда, когда [
коллинеарны тогда и только тогда, когда [ 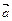
 ] =
] =  ? Если да, то почему?
? Если да, то почему?
6. Дан правильный ортонормированный базис 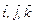 . Найти векторные произведения:
. Найти векторные произведения:
а) [[[[  ]
]  ]
]  ]
]  ], б) [(
], б) [(  –
–  )(
)(  +
+  )],
)],
в) [[(  –
–  )(
)(  +
+  )][(
)][(  +
+  )](
)](  –
–  )]].
)]].
7. При каких значениях 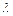 справедливо равенство:
справедливо равенство:
[  –
–  + 2
+ 2  , -3
, -3  + 3
+ 3  +
+ 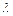
 ] =
] =  ?
?
- Что такое момент силы относительно точки?
9. Как определяется направление вектора магнитной индукции  в точке магнитного поля проводника с током?
в точке магнитного поля проводника с током?
- Как определяется направление силы Ампера?
- Как вычислить линейную скорость вращения точки вокруг неподвижной оси, зная угловую скорость?
Пример 1. Найти площадь  треугольника, построенного на векторах
треугольника, построенного на векторах  и
и  .
.
Решение. Найдем вектор  :
: 

Так как векторное произведение коллинеарных векторов равно нулевому вектору, то  Теперь, зная координаты
Теперь, зная координаты  и, учитывая, что длина вектора
и, учитывая, что длина вектора  равна площади параллелограмма, построенного на векторах
равна площади параллелограмма, построенного на векторах 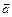 и
и 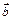 , найдем
, найдем
 Тогда
Тогда 
Пример 2. Зная вершину  квадрата
квадрата  , его центр
, его центр  и вектор
и вектор  перпендикулярный плоскости квадрата, найти остальные его вершины.
перпендикулярный плоскости квадрата, найти остальные его вершины.
Решение. Так как вектор  перпендикулярен как вектору
перпендикулярен как вектору  , так и вектору
, так и вектору 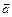 , то
, то  коллинеарен вектору
коллинеарен вектору  Кроме того,
Кроме того,  и так как векторы
и так как векторы  и
и 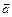 перпендикулярны, то
перпендикулярны, то  Следовательно,
Следовательно,  Зная координаты вектора
Зная координаты вектора  определим векторное произведение
определим векторное произведение

Так как  то
то  Поэтому вершины
Поэтому вершины  и
и  квадрата соответственно имеют координаты
квадрата соответственно имеют координаты  Так как точка
Так как точка  симметрична точке
симметрична точке  относительно начала координат
относительно начала координат 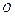 , то
, то 
Задачи
1. Выразить векторы [2 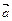 +
+  ,
, 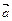 + 3
+ 3  ] и [
] и [ 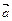 +
+  ,
, 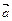 –
–  ] через [
] через [ 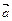
 ]. Найти их длины, если
]. Найти их длины, если 
2. Вычислить площадь параллелограмма, построенного на векторах  и
и  где
где  и
и  – единичные векторы, величина угла между которыми равна 600.
– единичные векторы, величина угла между которыми равна 600.
3. Найти площадь треугольника  , в котором
, в котором 
4. Найти единичный вектор  перпендикулярный: а) каждому из векторов
перпендикулярный: а) каждому из векторов  и
и  б) вектору
б) вектору  и оси абсцисс.
и оси абсцисс.
5. Вектор  перпендикулярный оси аппликат и вектору
перпендикулярный оси аппликат и вектору  образует острый угол с осью абсцисс. Зная, что
образует острый угол с осью абсцисс. Зная, что  найти его координаты.
найти его координаты.
6. Сила  приложена к точке
приложена к точке  Определить величину и направление момента этой силы относительно начала координат.
Определить величину и направление момента этой силы относительно начала координат.
7. Найти векторы  и
и  если
если 


8. Доказать тождество: [ 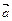
 ]2 + (
]2 + ( 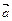
 ) =
) = 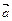 2
2  2.
2.
9. Прямая а проходит через точку А параллельно вектору 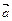 . Доказать, что расстояние от любой точки В до прямой
. Доказать, что расстояние от любой точки В до прямой  вычисляются по формуле:
вычисляются по формуле:

10. Даны точки 
 Доказать, что
Доказать, что  – квадрат. Найти вершины куба, для которого квадрат
– квадрат. Найти вершины куба, для которого квадрат  служит гранью.
служит гранью.
11. Найти вектор, являющийся ортогональной проекцией вектора  на плоскость, параллельную векторам
на плоскость, параллельную векторам 
Домашнее задание
1. Доказать, что если  то векторы
то векторы  – компланарны. Верно ли обратное утверждение?
– компланарны. Верно ли обратное утверждение?
2. Найти расстояние от точки С(3,2,–2) до прямой , проходящей через точки А(1,2,–3), В(5,2,0). Система координат – прямоугольная декартова.
3. Ребро куба ABCDA1B1C1D1 равно 1. Найти расстояние между диагональю куба и скрещивающейся с ней диагональю грани.
4. Дан тетраэдр, построенный на векторах  (2,0,0),
(2,0,0),  (3,4,0),
(3,4,0),  (3,4,2) (базис ортонормированный).
(3,4,2) (базис ортонормированный).
Найти: а) площади его граней, б) косинус угла между гранями АВС и ADC.
5. Доказать, что  .
.
Задачи повышенной трудности
1. Пусть  – площади граней тетраэдра,
– площади граней тетраэдра,  – соответствующие этим граням орты внешних нормалей. Доказать, что
– соответствующие этим граням орты внешних нормалей. Доказать, что 
2. Доказать теорему Мебиуса: В выпуклом пятиугольнике  площади треугольников
площади треугольников  равны
равны  Пусть
Пусть  – площадь пятиугольника. Доказать, что
– площадь пятиугольника. Доказать, что 
3. Докажите, что параллелепипед является прямоугольным тогда и только тогда, когда все его диагонали равны между собой.
4. Докажите, что прямоугольный параллелепипед  является кубом тогда и только тогда, когда его диагональ
является кубом тогда и только тогда, когда его диагональ  перпендикулярна плоскости
перпендикулярна плоскости  .
.
Тема5.3.Смешанное произведение векторов
Литература: [1], гл. 9, §3, стр.221–225; [2], гл.1, §3-5, стр.29–33; [27], гл.6, § 55, стр. 196-200.
Основные определения, теоремы и формулы
Смешанным произведением трех векторов  и
и  в ориентированном векторном пространстве называется скалярное произведение векторов
в ориентированном векторном пространстве называется скалярное произведение векторов 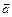 и
и  .
.
Геометрически смешанное произведение векторов интерпретируется как объем параллелепипеда, построенного на векторах как на сторонах, взятый со знаком плюс, если тройка векторов правая, и со знаком минус, если тройка векторов левая.
Смешанное произведение векторов  и
и  обозначается
обозначается  или
или  .
.
Теорема 1. Смешанное произведение векторов  и
и  равно нулю тогда и только тогда, когда эти векторы компланарны.
равно нулю тогда и только тогда, когда эти векторы компланарны.
Теорема 2. Если векторы  и
и  имеют координаты
имеют координаты  ,
,  относительно произвольно базиса
относительно произвольно базиса  , то
, то

Вопросы для самоконтроля
1. Что называется смешанным произведением:
а) некомпланарных векторов  , б) компланарных векторов
, б) компланарных векторов  ?
?
2. Сформулировать основные свойства смешанного произведения векторов.
3. Что можно сказать о векторах  если
если
а)  =0, б)
=0, б)  ,в)
,в) 
4. Что можно сказать о векторах  , если известно, что:
, если известно, что:
а)  б)
б)  , в)
, в)  , где
, где 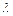 – некоторое вещественное число, г)
– некоторое вещественное число, г)  ?
?
5. Сравните  и
и  . В каком случае эти величины равны?
. В каком случае эти величины равны?
6. Пользуясь приведенной выше формулой для вычисления смешанного произведения векторов через их координаты в произвольном базисе  получите формулу для случаев, если базис: а) ортонормированный правый, б) ортонормированный левый.
получите формулу для случаев, если базис: а) ортонормированный правый, б) ортонормированный левый.
7. Найти вектор  удовлетворяющий условию
удовлетворяющий условию  где
где 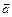 и
и 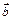 – данные векторы, а
– данные векторы, а  – данное число. Всегда ли уравнение имеет решение? Выясните геометрический смысл решения уравнения.
– данное число. Всегда ли уравнение имеет решение? Выясните геометрический смысл решения уравнения.
8. Верно ли, что для любых векторов  :
:
а) (  ) + (
) + (  ) + (
) + (  ) + (
) + (  ) + (
) + (  ) = 0,
) = 0,
б)  ?
?
Если нет, то, для каких векторов выполняется каждое из равенств а), б)?
Пример 1. Вычислить произведение 
Решение. Согласно свойствам векторные многочлены в смешанном произведении векторов перемножаются по тем же правилам, что и алгебраические многочлены. Тогда 
Произведения  равны нулю, а произведение
равны нулю, а произведение  следовательно,
следовательно, 
Пример 2. Вычислить объем тетраэдра, вершины которого находятся в точках 
Решение. Так как объем  тетраэдра, построенного на векторах
тетраэдра, построенного на векторах  равен 1/6 объема параллелепипеда, построенного на тех же векторах, то
равен 1/6 объема параллелепипеда, построенного на тех же векторах, то  Найдем координаты векторов
Найдем координаты векторов  Тогда
Тогда

Задачи
1. Вычислить смешанные произведения:
а)  б)
б)  если
если 
2. Вектор  перпендикулярен векторам
перпендикулярен векторам 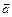 и
и  величина угла между которыми равна 300. Зная, что
величина угла между которыми равна 300. Зная, что  вычислить
вычислить 
3. Найти смешанное произведение векторов  (mage113-224.gif"> (1,–1,1),
(mage113-224.gif"> (1,–1,1),  (5,2,–3),
(5,2,–3),  (1,4,–2).
(1,4,–2).
3. Найти отношение объема параллелепипеда к объему тетраэдра, ребрами которого служат диагонали трех граней параллелепипеда, выходящие из одной его вершины.
4. Точки 
 и
и  делят ребра SA, SB и SC тетраэдра SABC в отношениях
делят ребра SA, SB и SC тетраэдра SABC в отношениях  = (SA, A’),
= (SA, A’),  = (SB,B’),
= (SB,B’),  = (SC,C’), где все числа
= (SC,C’), где все числа  положительны. Найти отношение объемов тетраэдров
положительны. Найти отношение объемов тетраэдров  и SABC.
и SABC.
Задачи повышенной трудности
1. Доказать, что объемы двух тетраэдров с равными трехгранными углами при одной вершине относятся как произведения ребер, сходящихся в вершинах этих углов.
2. Основанием пирамиды служит параллелограмм. В каком отношении делится объем пирамиды плоскостью, проходящей через сторону основания и среднюю линию противолежащей грани?
Тема 5.4. Уравнение фигуры. Приложение метода координат