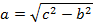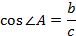Прямоугольник: определение, свойства, признаки.

Определение. Прямоугольник – это параллелограмм, у которого все углы прямые.

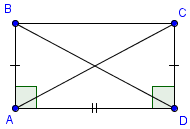Свойство 1. Диагонали прямоугольника равны.

Доказательство.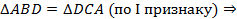

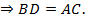
Теорема доказана.

Свойство 2. Любой прямоугольник вписывается в окружность, причём диагональ является диаметром этой окружности.

Доказательство. Сумма противолежащих углов равна 180°, а каждый угол прямой.

Теорема доказана.

Свойство 3. Площадь прямоугольника равна произведению двух прилежащих сторон.

Доказательство. Рассмотрение 3 случаев: целые, рациональные стороны и иррациональные стороны.

Теорема доказана.

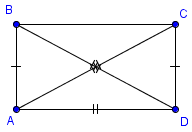
Признак 1. Если в параллелограмме диагонали равны, то этот параллелограмм – прямоугольник.

Доказательство.
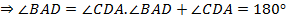, как в параллелограмме. Значит, они равны по 90°.

Теорема доказана.

Признак 2. Если параллелограмм вписывается в окружность, то этот параллелограмм – прямоугольник.

Доказательство. Противолежащие углы равны, как у параллелограмма, и в сумме дают 180°, как у вписанного четырёхугольника. Значит, все углы прямые, и это прямоугольник.

Теорема доказана.

2. Нахождение катета (a) и острых углов (∠A, ∠B) прямоугольного треугольника по данным гипотенузе (c) и другому катету (b).