Задание 4.
В пространстве даны точки А(-2;α1;1), B(3;α2;-1), C(5;α3;1), S(1;α1;0). Сделать чертеж пирамиды SABC и найти:
а) длину и уравнение ребра AB;
б) площадь и уравнение грани ABC;
в) высоту, проведенную из вершины S к грани ABC, и ее уравнение;
г) проекцию вершины S на плоскость ABC;
д) уравнение прямой, проходящей через вершину S параллельно ребру АВ;
е) уравнение плоскости, проходящей через вершину S параллельно грани АВС;
ж) уравнение плоскости, проходящей через ребро AS перпендикулярно грани АВС;
з) уравнение проекции ребра AS на грань АВС;
и) угол между ребрами АВ и AS;
к) угол между ребром AS и гранью АВС;
л) угол между гранями АВС и ABS;
м) координаты центра и радиус вписанной в пирамиду SABC сферы;
н) координаты центра и радиус описанной около пирамиды SABC сферы;
о) координаты центра (тяжести) пирамиды SABC;
п) объем пирамиды.
Задание 5.
Дана точка М(1;0;-2). Найти:
а) точку М1 (x1;y1;z1), симметричную точке М относительно точки S(α1;α2;α3);
б) точку М2 (x2;y2;z2), симметричную точке М относительно прямой
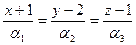 ;
;
в) точку М3(x3;y3;z3), симметричную точке М относительно плоскости
α1·x + α2·y+α3·z +1=0.