Задание 3.
Практические задания.
Индивидуальные условия заданий приведены в таблицах раздела 1 и определяются по номеру варианта n, а также с помощью параметров:
α1=-1-n (mod 7); α2=n (mod 5); α3 =-3-n (mod 3), где p (mod q) - остаток от деления p на q.
Задание 1.
На плоскости даны точки А(α1; α2-2) и В(α2-2;α2+4)
Найти:
а) точку C(x1;y1)-середину отрезка AB;
б) точку D(x2;y2), которая делит отрезок АВ в отношении p:q.
Параметры p,q приведены в табл. 1.1.
Таблица 1.1.
ПАРАМЕТРЫ p,q К ЗАДАНИЮ 1.
| n(mod 10) | p | q | n(mod 10) | p | q |
Задание 2.
На плоскости даны точки А (x1;y1), В (x2;y2) и С (x3;y3). Сделайте чертеж треугольника АВС и найдите:
а) длину и уравнение стороны ВС (записать общее уравнение,
каноническое, параметрическое и с угловым коэффициентом);
б) косинус угла А и угол А (в градусах);
в) уравнение прямой, проходящей через точку А параллельно
стороне ВС;
г) высоту, проведенную к стороне ВС и ее уравнение;
д) уравнение медианы, проведенной к стороне ВС;
е) уравнение биссектрисы угла А;
ж) координаты центра и радиус вписанной окружности;
з) координаты центра и радиус описанной окружности:
и) площадь треугольника;
к) координаты центра (тяжести) треугольника.
Таблица 1.2.
КООРДИНАТЫ ТОЧЕК А, В, С К ЗАДАНИЮ 2.
| N | x1 | y1 | x2 | y2 | x3 | y3 |
| -1 -7 -1 -5 -1 -5 -2 -3 -3 -9 -7 -2 -1 -7 -6 -5 -5 -1 -3 -7 -1 -3 -7 -5 -2 -4 -3 -2 -6 -1 -5 -3 -3 -4 -1 -1 -2 -3 -8 -3 -11 -14 -1 -6 -9 -7 -7 -3 -7 -3 -3 -8 -7 -13 -3 -2 | -1 -2 -1 -2 -6 -6 -11 -7 -4 -9 -1 -3 -6 -1 -1 -3 -8 -4 -1 -1 -9 -3 -8 -5 -2 -6 -9 -2 -6 -3 -2 -3 -6 -3 -1 -7 -1 -5 -1 -5 -2 | -1 -3 -1 -5 -5 -9 -7 -2 -7 -14 -7 -1 -9 -8 -4 -7 -8 -7 -1 -7 -2 -6 -2 -5 -11 -11 -3 -7 -1 -3 -7 -3 -7 -5 -4 -3 -6 -6 -3 -3 -3 -5 -5 -5 -1 -1 -1 | -1 -2 -2 -2 -6 -4 -2 -1 -4 -6 -9 -7 -1 -1 -1 -1 -3 -1 -3 -6 -2 -1 -3 -7 -6 -1 -6 -10 -5 -6 -1 -6 -9 -8 -3 -8 -1 -1 -7 -5 -11 -1 -4 -1 -1 -4 -1 -4 -3 | -5 -5 -4 -3 -7 -3 -7 -1 -11 -14 -9 -2 -8 -6 -1 -3 -3 -3 -4 -1 -7 -1 -7 -5 -14 -1 -3 -11 -3 -2 -5 -8 -6 -7 -3 -1 -2 -11 -1 -5 -7 -7 -3 | -1 -2 -1 -3 -3 -5 -1 -4 -8 -2 -3 -7 -1 -3 -1 -6 -3 -5 -9 -2 -11 -7 -7 -1 -1 -18 -4 -5 -6 -1 -9 -3 -6 -1 -4 -2 -2 |
Задание 3.
Решите планиметрическую задачу (см. табл.1.3.).
Таблица 1.3.
ЗАДАЧИ К ЗАДАНИЮ 3.
| n | Условие задачи. |
| На прямой 2x + y + 11=0 найти точку, равноудаленную от двух точек А (1;1),В (3;0) | |
| Найти координаты точки, симметричной точке (2;-4) относительно прямой 4x + 3y + 1=0 | |
| Найти уравнение диагонали параллелограмма, проходящей через точку пересечения его сторон x + y - 1=0 или y + 1=0, если известно, что диагонали параллелограмма пересекаются в точке В (-1;0) | |
| Составить уравнение прямой, проходящей через точку А(2;6) и образующей с осями координат треугольник, который находится во второй четверти и имеет площадь 3 кв.ед. | |
| Составить уравнение прямой, проходящей черев точку А(-1;2) так, что середина ее отрезка заключенного между параллельными прямыми х + 2y + 1=0 и x + 2у - 3 = 0, лежит на прямой х - у - 6 =0 | |
| Даны уравнения двух сторон треугольника 4х-5у+ 9=0 и х + 4у -3=0. Найти уравнение третьей стороны, если известно, что медианы этого треугольника пересекаются в точке (3;1) | |
| Вычислить координаты вершин ромба, если известны уравнения двух его сторон 2х - у+4=0 и 2х – у + 10=0 и уравнение одной из него диагоналей х + у + 2=0 | |
| Составить уравнения сторон треугольника, если А(-5;5), В(3;1) - две его вершины, а D(2;5) -точка пересечения его высот | |
| Дано уравнение одной из сторон квадрата х + 3у – 7=0 и точка пересечения его диагоналей Р(0;-1). Найти уравнения трех остальных сторон этого квадрата | |
| Даны уравнения одной ид сторон ромба х - 3у + 10 =0 и одной из его диагоналей х + 4у - 4=0. Диагонали ромба пересекаются в точке Р(0; 1). Найти уравнения трех остальных сторон ромба | |
| Уравнения двух сторон параллелограмма х + 2у + 2=0 и х + у – 4=0, а уравнение одной из диагоналей x – 2=0 . Найти координаты вершин | |
| Даны вершины А(-3;-2) и В(8;-4) трапеция АВСD (АГ || ВС). Известно, что диагонали трапеция равны и точка пересечения диагоналей. О(0;2). Найти координат вершин С и 1) этой трапеции | |
| Даны вершины А(2;-2) и В(-1) и точка Р(1;0) пересечения медиан треугольника. Составить уравнение высоты треугольника, проведенной через третью вершину С | |
| Даны уравнения двух высот треугольника 3х + 2у- 34=0 и х + у – 1=0 и одна из вершин А(6; 5). Составить уравнения сторон | |
| Даны уравнения двух медиан 2х -11y+ 28=0 и 5х + 7у – 22=0 и одна из вершин (-2;-2) треугольника. Составить уравнения сторон | |
| Две стороны треугольника заданы уравнениями 2х+ + у - 1 =0 и х - 3у +14=0, а середина третьей стороны совпадает с началом координат. Составить уравнение третьей стороны | |
| Даны уравнения сторон треугольника: (АВ) 7х - 2у + 32=0;(АС) x + у + 2 =0 ; (ВС) 4х + у - 1=0. Найти точку пересечения его высот | |
| Составьте уравнения катетов прямоугольного равностороннего треугольника, если уравнение гипотенузы 3х - у + 11=0 и С (4;3) - вершина прямого угла | |
| В равнобедренном треугольнике известны: уравнение основания 5х 4 - 63 =0, уравнение одной из боковых сторон х + 4у – 14=0 и точка на второй боковой стороне (3;7). Найдите уравнение второй боковой стороны | |
| Одна и сторон квадрата лежит на прямой х -5y+32=0, а одна из вершине находится в точке (2;1). Найдите уравнения остальных сторон квадрата | |
| Составить уравнения трех сторон квадрата, если известно, что четвертой стороной является отрезок прямой 4х - 7у + 28=0, концы которого лежат на осях координат | |
| Точки К (1;3) и L (-1;1) являются серединами оснований равнобедренной трапеции, а точки Р (3;0) и Q (-3;5) лежат на ее боковых сторонах. Составить уравнения сторон трапеции | |
| Даны стороны треугольника: (АС) 2х - 15у – 55= 0; (АВ) 4x- 3у + 25=0; (BC) 14х + 3у- 61 - 0. Составить уравнение прямой, проходящей через вершину С и черев точку на стороне АВ, делящую ее (считая от вершины А) в отношении 1:4 | |
| Точки В (7;1) и D (9;-3) являются противоположнымивершинами квадрата. Определить координаты двух других вершин | |
| В треугольнике известны уравнения высоты х + у- 3=0 и медианы х - 4у + 10=0, проведенных из различных вершин. Написать уравнения сторон треугольника, зная одну его вершину (8;9) | |
| Написать уравнение сторон треугольника, зная одну его вершину (6;3), уравнения высоты х - 9у + 75=0 и биссектрисы х - 13у +79=0, проведенных из одной вершины | |
| Точка А (2;0) является вершиной правильного треугольника, а противолежащая ей сторона лежит на прямой х + у -1=0. Составить уравнения двух других сторон | |
| Длина стороны ромба с острым углом 60° равна 2. Диагонали ромба пересекаются в точке М (1;2), причем большая диагональ параллельна оси абсцисс. Составить уравнения сторон ромба | |
| Точка А (1;2) является серединой одного из оснований прямоугольной трапеции, а точка В (3;-1) - серединой средней линии. Боковая сторона, перпендикулярная основаниям, лежит на прямой 4х - 3у + 10=0. Составить уравнения остальных сторон трапеции | |
| Написать уравнения сторон треугольника, зная одну его вершину (9;2), уравнения биссектрисы х + у- 5=0 и медианы х - у =0, проведенных из различных вершин | |
| Даны координаты двух вершин треугольника А (-1;3), В (2;5) и ортоцентр - точка Н (1;4). Найти координаты третьей вершины треугольника. Ортоцентром треугольника называется точка пересечения его высот. | |
| Точка Н (-3;2) является точкой пересечения высот треугольника, две стороны которого лежат на прямых 2х-у=0 и х + у- 3=0. Составить уравнение третьей стороны | |
| Найти радиус и координаты центра окружности, проходящей через точку А (-1;3) и касающейся прямых 7х + у =0 и х - у + 8=0 | |
| Окружность проходит через точки М (1;0) и N (2;1). Найдите центр этой окружности, если известно, что он лежит на прямой 5х - у -4=0 | |
| Точки В (1;2) и С (3;-6) симметричны относительно некоторой прямой. Составить уравнение этой прямой | |
| Диагонали параллелограмма пересекаются в точке К (-2;4). Составить уравнение диагонали, не проходящей через точку пересечения сторон 4х - у + 4=0 и 4х + 3у + 20=0 | |
| Площадь прямоугольного треугольника, катетами которого является оси координат, равна 8. Составить уравнение гипотенузы, если известно, что они проходит через точку А (-4;8) | |
| Составить уравнение прямой L1, параллельной прямойL2:2х + 3у – 23=0, если середина отрезка прямой L3: 5х + 2 + 3=0,заключенного между параллельными прямыми L1 и L2 лежит на прямой L4: 5х - у + 24=0 | |
| Составить уравнение стороны треугольника, в котором известны точка пересечения медиан (-1;7) : уравнения двух других сторон x + 4у -37=0, 2х - у +16=0 | |
| Даны две стороны х - у + 5=0 и х – у + 10=0 диагональ 3х + у -10=0 ромба. Найти вершины ромба | |
| В треугольнике известны две вершины А (-2;9), В (2;-3) и точка пересечения высот О (2;7). Написать уравнения сторон | |
| Точка А (3:-2) является вершиной квадрата, а точка М(1;1) - точкой пересечения его диагоналей. Составить уравнения сторон квадрата | |
| Даны уравнения одной ив сторон ромба х + у - 39=0 и одной из его диагоналей х-3у+11=0. Найти уравнения остальных сторон ром ба, если его центр - точка N (-2;3). |
| Найти координаты вершин параллелограмма, в котором известны две стороны 2х - 5у – 5=0 и 2х + 5у – 15=0 и диагональ 6х + 5у – 35=0 | |
| Найти координаты точек С и D четырехугольника АВСD, в котором отрезки АВ и DС параллельны, BD и АС перпендикулярны друг другу и заданы вершины А(9;-1), В (0;5) | |
| Даны две вершины (3;-1), (1;4) и центр тяжести (0-.2) треугольника. Найти координаты третьей вершины треугольника и составить уравнения его сторон | |
| Даны уравнения двух высот треугольника 3х + 4у - 23 =0 и 12х - 5у - 24 =0 и одна из его вершин (1;1). Составить уравнения сторон | |
| Написать уравнения сторон треугольника, две медианы которого лежат на прямых х + у - 3 = 0 и 2х +3у -1=0, а точка А (1;1) является вершиной треугольника | |
| Две стороны треугольника заданы уравнениям: х + 3у - 21=0 и 7х + у + 13 = 0, середина третьей стороны - точка (2;3). Составить уравнение третьей стороны | |
| Даны уравнения сторон треугольник: (NM) 3х - 5у+ +17=0, 8x + 6у – 32=0, (NР) 5х + 11у + 9=0. Найти ортоцентр треугольника. (Ортоцентром треугольника называется точка пересечения его высот) | |
| Гипотенуза прямоугольного треугольника лежит на прямой 2х + у -2=0, а точка С (3;-1) является вершиной прямого угла. Площадь треугольника равна 9/4. Составить уравнения прямых, на которых лежат катеты | |
Основание равнобедренного треугольника лежит на прямой х + 2у-2=0, а одна из боковых сторон - на прямой у + 2х – 1=0. Составить уравнение другой боковой стороны треугольника, зная, что её расстояние от точки пересечения данных прямых равно 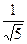
| |
| Составить уравнения сторон квадрата, в котором одна из вершин - точка (8;7) и одна из сторон лежит на прямой 5х + 2у + 4=0 | |
| Составить уравнения трех сторон квадрата, если известно, что четвертой стороной является отрезок прямой 2х + у – 8=0, концы которого лежат на окружности (х -3)2+y2= 4 | |
| Точки М(3;7) и. N (2;3) являются серединами оснований равнобедренной трапеции. Точки К(1;7 ) и Р(4;6,5) лежат на ее боковых сторонах. Составить уравнения сторон трапеции | |
| Даны стороны треугольника: (АВ) 4х + 3у - 10 =0; (ВС) 8х + 2у - 8 =0; (АС) 8х + 5у – 18=0. Составить уравнение прямой, проходящей через точку С и долящей сторону АВ в отношении 2:3 (считая от вершины А) | |
| Противоположными вершинамиквадрата являются точки (-5;-3) и (3;17). Найти координаты двух других вершин | |
| Написать уравнения сторон треугольника, зная одну его вершину (2;7), уравнение медианы 9х +у + 4=0 и высоты х + 3у – 11=0, проведенных из различных вершин | |
| Написать уравнения сторон треугольника, зная одну его вершину (-5;4), уравнения высоты 6х + у – 61=0 и биссектрисы 4х - 3у + 7=0 | |
| Точка М(6;4)является вершиной правильного треугольника, а противолежащая ей сторона лежащего на прямой 3х – у + 2 = 0. Найти уравнения остальных сторон треугольника. | |
| Длина стороны ромба с тупым углом 120° равна 6/2. Меньшая диагональ параллельна биссектрисе 2 и 4 координатных углов. Диагонали пересекаются в точке (-4:6). Составьте уравнения сторон ромба | |
| Точка Р(8;1) является серединой одного из оснований прямоугольной трапеции, а точка N(2:3) - серединой средней линии. Боковая сторона, перпендикулярная основаниям, лежит на прямой 4х + 3у +1=0. Составить уравнения сторон | |
| Составьте уравнения трех сторон треугольника, в котором медиана 3х + 2у – 6=0 и биссектриса х – у =0 проведены не из вершины (4;0), а из двух других вершин | |
| Даны стороны треугольника: 4х - 3у + 26 =0 (АВ); х + 2у + 1=0 (АС); 7x+ 3у-37=0 (ВС). Найти точку пересечения медианы, проведенной из вершины В и высоты, преходящей через вершину С | |
| Найти радиус и координаты центра окружности, проходящей через точку А(-1;8) и касающейся прямых х + 10=0 и 4х-3у+10=0 | |
| Точка К отстоит на одинаковых расстояниях от точек Р(7;8) и Q (1;2). Найти координаты точки К, если известно, что она лежит на прямой 4х - 5у + 27=0 | |
| Найти координаты точки N симметричной точке М относительно прямой х + у - 5 =0. Точка М отстоит от прямой на расстоянии вдвое большем, чем точка К (-2;7) и находится с ней по одну сторону от прямой, причем отрезок КМ перпендикулярен прямой | |
| В параллелограмме две стороны заданы уравнениями х - 5у + 7=0 и 5х – 3 у - 9=0. Составить уравнение диагонали параллелограмма, не проходящей через точку пересечения этих сторон, если известно, что диагонали пересекаются в точке М(2;4) | |
| Найти координаты вершин треугольника, симметричного треугольнику АВС относительно центра описанной около треугольника АВС окружности, если А( 9;-1) В(5;1), С(0;-5) | |
| Составить уравнение прямой, перпендикулярной прямой х + 3у-13=0 и образующей с осями координат треугольник, площадь которого равна 6 |
| Составить уравнение прямой, проходящей через точку А(1;2) так, что отрезок этой прямой, заключенный между прямыми 3х + у + 2=0 и 4х + у – 1=0, в точке А делится пополам | |
Центр тяжести треугольника - точка (  ; ; 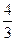 ).
Уравнения двух его сторон 4х + у + 14=0 и
- 6y - 9=0. Составить уравнение третьей стороны ).
Уравнения двух его сторон 4х + у + 14=0 и
- 6y - 9=0. Составить уравнение третьей стороны
| |
| Известны уравнения двух сторон ромба 7х - 9y - 39 =0 и 3х + 11y -91=0 и одной из его диагоналей 5х + у - 13=0. Вычислить координаты вершин ромба | |
| Составить уравнение третьей стороны треугольника, если известны уравнения двух его сторон 6х - у - 11=0 и 4х + 5у + 13=0 и ортоцентр- точка (-1;2) | |
| Написать уравнения сторон квадрата, центр которого - точка (1-3), а одна из вершин - точка (-4:7) | |
| Написать уравнения сторон ромба, если известны диагональ х + у – 2=0, точка её пересечения с другой диагональю (0;2) и одна из сторон 3х - у – 10=0 | |
| Вычислить координаты вершин параллелограмма, в котором две стороны лежат на прямых 2х - 5у- 5=0 и 2х + 5у -15=0, а одна из диагоналей на прямой 6х + 6у - 35=0 | |
| Диагонали трапеции ABCD (АD || BC) перпендикулярны друг другу и заданы вершины А (4;-1) и В(iЗ;6). Найти координаты вершин C и D трапеции | |
Составить уравнения сторон треугольника, в котором даны две вершины (-7;6) и (7;4) и точка пересечения отрезков, соединяющих эти вершины с серединами противоположных сторон 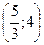
| |
| Даны уравнения двух высот треугольника x - 5у + 16 = 0 и 9x + 7у + 14=0 и одна из ёе вершин (-6:-З). Написать у равнения сторон треугольника | |
| Даты уравнения двух медиан 3x+ 3y+2=0 и 2х + 2у – 21=0 треугольника и одна из вершин М(5;-1). Найти уравнения сторон треугольника | |
| Середина одной из сторон треугольника - точка (0;3).Две другие стороны лежат на прямых х - 9у + 52= 0 и х + у – 8= 0. Составить уравнение третьей стороны | |
| Найти точку пересечения высот треугольника, стороны которого лежат на прямых 6х + у – 23=0, 9х - 4у – 7=0, 3х - 5у – 17=0 | |
| Точка С (6;1) - вершина прямого угла в треугольнике, а гипотенуза лежит на прямой 2х-3у+5=0. Написать уравнения катетов, один из которых лежит на прямой, содержащей точку (-4;-25). |