II. График гиперболы

1. Симметрия.
Гипербола имеет две оси симметрии – ось Ox и ось Oy; и центр симметрии – начало координат O(0;0).

2. Вершины. Действительные и мнимые оси.

Вершины гиперболы – это точки пересечения гиперболы с осями симметрии, т.е. с осью Ox и осью Oy.

С осью Ох: у=0 ,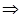

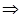
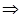
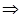
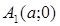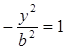
С осью Оу: х=0 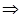нет действительных корней, гипербола не пересекается с Оу.

Итак, две вершины: 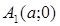и .

Опр.Отрезок А₁А₂ и его длина 2а называется действительной осьюгиперболы.

Возьмем на оси Оу две точки и .

Опр.Отрезок В₁В₂ и его длина 2b называется мнимой осьюгиперболы.

а – действительная полуось, b – мнимая полуось гиперболы.

 

3. Асимптоты гиперболы

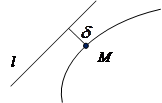Опр. Прямая называется асимптотой кривой, если расстояние от точки М кривой до этой прямой стремится к нулю при удалении точки М вдоль кривой в бесконечность.

Гипербола имеет две асимптоты:

, – уравнение асимптот гиперболы.

4. График гиперболы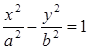

1) Построить (характеристический) прямоугольник со сторонами, параллельными осям Ох и Оу и проходящими на оси Ох на расстоянии а от точки О(0;0) по обе стороны, на оси Оу – на расстоянии b.

2) Провести асимптоты гиперболы по диагоналям прямоугольника.

3) Вершины гиперболы в точках 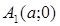и и построить график гиперболы

 

 

А₁, А₂ – вершины гиперболы, – фокусы гиперболы.