III. Каноническое уравнение прямой
Глава 3. Аналитическая геометрия на плоскости и в пространстве
Прямая линия на плоскости
I. Уравнение прямой, проходящей через данную точку перпендикулярно заданному вектору
|
| y |
| x |
 (  ;  )
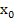M (x; 
|
| l |
| 0 |
(1) –уравнение прямой, проходящей через точку М0(x0;y0) и ⊥ .
Опр. Вектор 
, перпендикулярный данной прямой, называется нормальнымвектором прямой. Из (1) видно, что уравнение прямой – это уравнение первой степени (линейное) относительно текущих координат х и у.
Пример 1.1. Найти уравнение прямой, проходящей через точку М0(-1;2) и 
.
II. Общее уравнение прямой.
Ax+By+C=0 (2) –общее уравнение прямой, где 
- нормальный вектор.
III. Каноническое уравнение прямой
| M0(x0;y0) |
|
| M(x;y) |
(3) – каноническое уравнение прямой (через точку М0(х0;y0)и параллельно вектору 
), 
– направляющий вектор прямой.