Полярные координаты
 Пусть на плоскости дана точка О – полюс и луч ОР – полярная ось. Тогда положение точки М на плоскости определят полярный угол
Пусть на плоскости дана точка О – полюс и луч ОР – полярная ось. Тогда положение точки М на плоскости определят полярный угол 
 и радиус-вектор
и радиус-вектор
r =  . Если полярная ось совпадает с осями координат хОу, то
. Если полярная ось совпадает с осями координат хОу, то
x = rcos 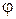 , y = rsin
, y = rsin 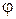 (51)
(51)
и обратный переход
r =  , tg
, tg 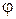 = y/x. (52)
= y/x. (52)
Если полюс совпадает с фокусом эллипса, гиперболы, параболы и луч ОР направлен по оси симметрии в сторону более удаленной вершины, то уравнения всех трех кривых будут одинаковы
 , (53)
, (53)
где  – эксцентриситет, р – параметр. Для эллипса и гиперболы р = b2/a.
– эксцентриситет, р – параметр. Для эллипса и гиперболы р = b2/a.
Уравнение типа (53) r = r( 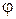 ) называется полярным уравнением. Для построения графика такой функции из полюса проводят лучи с шагом
) называется полярным уравнением. Для построения графика такой функции из полюса проводят лучи с шагом  и откладывают точку на расстоянии r от полюса.
и откладывают точку на расстоянии r от полюса.
Решение типичных задач
 Пример 18. Привести уравнение x2 + y2 = 4x к каноническому виду. Записать для него полярное уравнение и построить кривую.
Пример 18. Привести уравнение x2 + y2 = 4x к каноническому виду. Записать для него полярное уравнение и построить кривую.
Решение. Выполним приведение к полному квадрату: (x – 2)2 + y2 = 4. Это уравнение окружности с центром в (2; 0), R = 2. Переход к полярному уравнению:
r2cos2 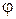 + r2sin2
+ r2sin2 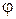 = 4rcos
= 4rcos 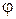
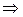 r = 4cos
r = 4cos 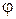 ,
,  .
.
Пример 19. Построить график функции  в полярной системе координат по точкам. Значение угла менять от 0 с интервалом
в полярной системе координат по точкам. Значение угла менять от 0 с интервалом  . Найти уравнение в прямоугольной системе координат.
. Найти уравнение в прямоугольной системе координат.
Решение. Функция четная 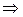 график симметричен относительно Ох.
график симметричен относительно Ох.
 Имеется точка разрыва
Имеется точка разрыва  . Составим таблицу значений функции.
. Составим таблицу значений функции.
| j | p/8 | p/4 | 3p/8 | p/2 | 5p/8 | 3p/4 | 7p/8 | p |
| r | 3,6 | 2,6 | 2,5 |
Проведем лучи для всех значений 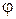 и на расстоянии r от центра вдоль них выделим нужные точки, последовательно соединим их и получим график параболы.
и на расстоянии r от центра вдоль них выделим нужные точки, последовательно соединим их и получим график параболы.
Для перехода от r, 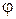 к х, у используем соотношения:
к х, у используем соотношения:  ,
,  ,
,  . Тогда
. Тогда  =
=  и
и 
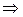
 = 5
= 5  или
или  = х + 5. Возведем в квадрат и получим x2 + y2 = (х + 5)2
= х + 5. Возведем в квадрат и получим x2 + y2 = (х + 5)2 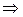 y2 = 10(х + 2,5) уравнение параболы.
y2 = 10(х + 2,5) уравнение параболы.
Задачи для самостоятельного решения
Построить графики следующих функции в полярной системе координат по точкам. Значение угла менять от 0 с интервалом, указанным в квадратных скобках. Найти уравнения в прямоугольной системе координат.
31)  , [
, [  /8]; 32)
/8]; 32)  , [
, [  /8];
/8];
33)  , [
, [  /8]; 34)
/8]; 34)  , [
, [  /12];
/12];
35)  , [
, [  /8]; 36)
/8]; 36)  , [
, [  /12];
/12];
37)  , [
, [  /12]; 38)
/12]; 38)  , [
, [  /12];
/12];