Лекция.

Таќырыбы: Вектор ұғымы. Векторларға қолданылатын сызықтық амалдар.

1-анықтама. Вектор дегеніміз бағытталған кесінді немесе қайсысы бірінші (басы), ал қайсысы екінші (ұшы) екендігі көрсетіліп берілген нүктелер жұбы.

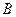Вектор ұзындығымен және бағытымен анықталған геометриялық объект. Егер вектор басы нүктесі және ұшы нүктесі арқылы берілетін болса, онда оны 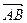немесе 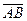деп белгілейді. Көпшілік жағдайда, вектор бір ғана әріппен белгіленеді, мысалы 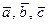, т.с.с.

2-анықтама.Вектордың модулі немесе ұзындығы деп оның басы мен ұшының ара қашықтығын айтады. Кейбір жағдайларда вектордың ұзындығы оның абсолют шамасы деп те атайды. Вектордың модулі 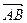, немесе 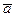деп белгіленеді.

3-анықтама. Егер екі немесе одан да көп векторлардың бастары бір нүктеде түйіскен болса, ондай векторлар үйлескен деп аталады (1.1а-сурет).

4-анықтама.Вектордың бас нүктесі мен соңғы нүктесі үйлескен болса, ол вектор нөльдік вектор деп аталады. Нөльдік вектордың бағыты анықталмаған, яғни кезкелген бағытты қабылдайды. Нөльдік векторды түрінде белгілейміз.

Ескерту: Қарастырылатын векторының бас нүктесі үшін кеңістіктегі немесе жазықтықтығы кезкелген нүктені (қажеттілігіне қарай) алуға болады. Сондықтан, олар да бос немесе ерікті векторлар деп атайды. Алдағы уақытта қарастырылатын векторларды ерікті векторлар деп түсіну қажет.

5-анықтама.Бір түзудің немесе параллель түзулердің бойында жатқан векторлар өзара коллинеарлы деп аталады (1.1б-сурет).

6-анықтама.Өзара коллинеарлы, ұзындықтары мен бағыттары бірдей және векторлары тең векторлар деп аталып, 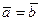түрінде жазылады (1.1в-сурет).

7-анықтама. Өзара коллинеарлы, ұзындықтары бірдей, ал бағыттары әр түрлі, және векторлары қарама-қарсы векторлар деп аталады және 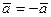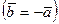түрінде жазылады.

8-анықтама.Векторлардың біреуін екіншісімен дәл келгенше бұрғандағы ең кіші айналу бұрышын ( 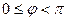) сол екі вектордың арасындағы бұрыш деп атайды. Аралық бұрыш, векторды сағат тіліне қарсы бағытпен айналдырудан шыққан болса оң, ал сағат тілімен бағыттас айналдырудан шыққан болса теріс болады.

9-анықтама. 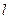осіндегі бағытталған 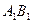кесіндісінің шамасы 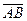векторының 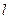осіне проекциясы деп аталады да (1.2а-сурет), былай белгіленеді: 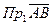. Демек,

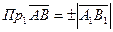
Теорема. 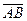векторының 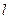осіне проекциясы осы вектордың ұзындығын оның 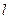осімен жасайтын бұрышының косинусына көбейткенге тең.

.

В

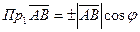
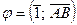A В

А1

1.2-сурет.

Дәлелдеуі.Егер болса, онда 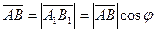(1.2а-сурет), ал егер 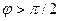болса, онда 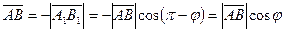(1.2б-сурет).

10-анықтама.Векторлар бір жазықтыққа параллель болса, онда олар компланар векторлар деп аталады.

11-анықтама. векторының 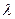санына көбейтіндісі деп модулі векторының модулі мен 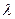санының модулінің көбейтіндісіне тең, ал бағыты 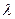>0 болғанда, векторының бағытымен бағыттас немесе 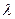<0 болса, оған қарама-қарсы бағытта болатын векторын айтады (1.3-сурет). Егер болса, онда 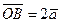, ал 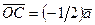. Егер векторды 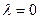санына көбейтсек, нөльдік вектор болады, ал 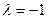санына көбейтсек модулі векторының модуліне тең және бағыты оған қарама-қарсы бағытталған - векторы пайда болады. Векторды санға көбейту анықтамасынан мынадай теореманың дұрыстығы шығады.

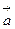
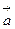-1/2 2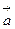

С 0 А В 1.3-сурет.

Теорема: және векторының коллинеар болуы үшін, теңдігі орындалатындай жалғыз ғана 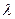санының болуы қажетті және жеткілікті.

Векторларға сызықты амалдар қолдану. Векторларға сызықты амалдар қолдану қатарына, векторларды қосу, азайту және векторды нақты санға көбейту амалдары жатады.

Векторларды қосу. Берілген және векторларының қосындысыдеп, векторының соңғы нүктесіне бағытын сақтай отырып, векторын үйлестіргеннен кейінгі векторының басы мен векторының соңын қосатын векторын айтамыз, яғни (1.4а сурет).

Бұл анықтама, векторлар коллинеарлы болмаған жағдайда, «үшбұрыштар ережесің деп аталады.

Екі және векторларының қосындысы деп, олардың, бағыттарын сақтай отырып, бас нүктелерін үйлестіру арқылы құрылған параллеограмның үйлесу нүктесінен басталатын диагональ вектор -ны айтамыз және бұл «параллеограмм ережесің деп аталады (1.4б-сурет).

Жалпы жағдайда, векторларының қосындысын алу үшін біріншісінен бастап ұзындықтары мен бағыттарын сақтай отырып, тізбектеп жалғау арқылы, бірінші вектордың бас, n-ші вектордың соңғы нүктелерін қосып, «көпбұрышты тұйықтау ережесінң қолданамыз (1.4в-сурет).

Енді векторларды қосу амалына қарасты қасиеттерді келтірейік:

1). (ауыстырымдылық заңы);

2). (терімділік заңы);

3.)

4). Кез келген векторына қарама-қарсы векторы табылып, теңдігі орындалады.

Енді келтірілген қасиеттердің дұрыстығына көз жеткізейік.

Векторларды қосудың 3) қасиеті нөльдік вектордың анықтамасынан оңай шығады. Ал в) қасиеттің дұрыстығын көрсету үшін өзара коллинеарлы, және векторларына, векторлардың қосындысының анықтамасын еске алсақ, олардың ұзындықтары бірдей, бағыттары қарама-қарсы болғандықтан, өзара жойылып, қосындысы нөльдік векторды беретіндігін көруге болады.

 

 

Сурет.

Ауыстырымдылық заңын дәлелдеу үшін «параллеограмм ережесінң қолданайық (1.5а-сурет).

Ол үшін

(1.1)

(1.2)

Бұдан (1) және (2) теңдіктердің сол жақтары өзара тең, ендеше оң жақтары да тең, яғни

Терімділік 2) заңын дәлелдеу үшін тағы да векторлардың қосындысын пайдаланамыз. Жоғарыдағы (1.5б-суреттен):

Сурет.

(1.3)

(1.4)

Бұл алынған (3) және (4) теңдіктердің сол жақтары тең, ендеше,

.

Векторларды азайту. Екі және векторларының айырымы – деп, векторымен қосындысы векторына тең болатын векторын айтамыз, яғни . Бұдан теңдігін аламыз.

Екінші сөзбен айтқанда, векторлар айырымын алу үшін, векторына қарама-қарсы – « ң векторын алып, векторымен қосындысын қарастырамыз, яғни теңдігін аламыз.

Екі вектордың айырманың геометриялық кескінін салу үшін жоғарыдағы негізгі анықтама бойынша, «үшбұрыш ережесінң қолданамыз, яғни векторына векторын қосу арқылы векторын аламыз (1.6- сурет).

 

Сурет.

Суретке зейін салып қарасақ, айырымы боатын векторы, бастары үйлескен және векторларын қосатын кесіндінің бағыты азайтқыш вектордың соңғы нүктесінен бағытталатындығын көреміз.

Векторды нақты санға көбейту. Векторды нақты санға көбейту санға көбейту деп, берілген векторымен коллинеар, ұзындығы есе өсетін және бағыты, егер >0 болса, векторымен бағыттас; <0 болса, векторымен қарама-қарсы болатын, векторын айтамыз.

Екінші сөзбен айтқанда, егер болса, берілген векторының ұзындығы есе өзарады, болса, есе қысқарады.; болса, берілген вектордың ұзындығы сақталады.

Түсінікті болу үшін =2, =-2, = , =- , =1, =-1 болғандағы векторының өзгеруін көрсетейік (1.7-сурет).