Лекция.

ЛЕКЦИЯ ТЕЗИСТЕРІ

Таќырыбы: Жазықтықтағы координаталар жүйесі. Жазықтықтағы аналитикалық геометрияның қарапайым есептері.

Түзудін бойынан еркімізше бір О нүктесін алсақ, онда сол түзудін бойындағы кез келген М нүктесі ОМ кесінді аркылы анықталады. Бұл М нүктесі О нүктесінің не оң, не сол жағында жатуы мүмкін. М нүктесінің О нүктесіне қатысты екі жағдайын қарастырайық. О нүктесінін сол жағындағы нүктені М1 оң жағындағы нүктені М2 деп белгілейік (1-сызба).

Егер О нүктесінен оңға қарай алынған ОМ2 кесіндісін оң таңбалы болсын десек, он­да О нүктесінен солға карай алынған ОМ1 кесіндісі теріс танбалы болады. Мұндай өзінің ұзындығымен және таңбасымен сипатталатын кесінді бағытталған кесінді деп ата­лады.,

Егер m белгілі бір бірлік өлшемі үшін алынса, онда әрбір кесінді осы бірлік арқылы өлшенеді, яғни берілген ОМ кесіндісінің m бірлік өлшемге қатынасынан бір сан шығады:

 

Берілген кесіндіні өлшейтін m бірлік өлшемді масштаб деп атаймыз. Масштаб m=1болса, онда х = ОМ. Егер М нүктесі М1 жағдайда болса, онда х теріс таңбалы сан болады:

Егер М нүктесі М2 жағдайда болса, онда х он таңбалы сан бо­лады:

Түзудін бойындағы кез келген нуктені аңықтайтын шарттардың киындысын түзудің бойындағы координаталар жүйесі дейміз. Қарастырылып отырған жағдайдағы кез келген нүкте (М) координатаның бас нүқгесінен (О) сол нүктеге (М) дейінгі қашықтықтың масштабқа қатынасымен анықталады. Түзудің бойындағы мұндай координаталар систем асы декарттың координаталар жүйесі деп аталады.

Түзудің бойындағы кез келген М нүктесінің координатасын х деп атасақ, онда осы нүкте мен оның координатасының өз ара сәйкестігін мынаңдай символмен белгілейміз: М(х). Бүл символ М нүктесінің координатасы х болады деген мағынаны береді, яғни М нүктесі х координатасы арқылы берілді деп ұғу керек. Сонымен, түзудің бойындағы кез келген нүкте жалғыз санмен аныкталады, яғни бір нүктеге бір-ақ сан сәйкес, керісінше айтқанда, бір санға ылғи бір нүкте сәйкес келеді.

Егер х-тің мәні нольден бастап оңға қарай түзудін бойымен шексіз өсе берсе, онда х айнымалы шама болады, ал оның өзгерілуін мынандай белгімен жазамыз: х = 0, х= + ∞ , яғни 0 < х < + ∞. Сол сияқты айнымалы шама нольден бастап солға қарай шексіз кемитін болса, онда былайша белгіленеді: х = 0, х = - ∞, яғни - ∞ < х < 0 немесе 0 > х > - ∞.

Енді түзудің бойындағы х-тің толып жатқан сансыз мәндерін жалпы түрде белгілeyгe болады: - ∞ < х < + ∞

Бас нүктенін координаталары ылғи нольге тең, яғни О(0), х = 0. «Нүктені табуң деген сөзді онын ылғи «координатасын табуң деген мағынада түсіну керек.

х координатасының мәні (1) қатынасымен аныкталатынын көрдік. Ал координатаны сызбада көрсету үшін оны былайша жазуға болады:

ОМ=х (1///)

Бұл жағдайда ОМ=х бағытталған кесінді емес, сол бағытталған кесіндіні өлшейтін сан. Өйткені мұнда алынып отырған мас­штаб ылғи бірге тең (m=1) және осыған сәйкес нүктелердің координаталарын бірыңғай бір координаталар жүйесымен алып отырмыз.

Түзуге он бағыт беріліп, оның бойынан бір О нүктесі белгіленіп және бірлік өлшем — масштаб алынса, онда мүндай түзу координаталық ось деп атала­ды (1-сызба). Түзудің оң бағыты көрсетілсе (2-сызба), онда ол ось деп аталады.

Координаталык горизонталь осьті абсцисса ocі деп, оны x әрпімен белгілейік (1-сызба).

Кесіндіден екі бас әріппен белгілейміз: М1, М2. Осы екі нүктенің бірін (М1) кесіндінің бастапқы нүктесі десек, екіншісін (М2) соңғы нүктесі дейміз.

Кесіндінің бағыты осьтің бағытыменбірдей, яғни ңүктенің қозғалысы бас нүктеден онға қарай саналады. М1, М2 және М2М1 кесінділердің ұзындықтары бірдей, ал бағыттары әр түрлі, таңбалары қарама-қарсы. Өзінің ұзындығымен және таңбасымен сипатталатын кесіндіні бағытталған кесінді дегенбіз. Бағытталған кесінділер былайша белгіленеді: М1М2, М2М1. Бағытталған кесіндінің ұзындығы модуль деп аталады. Осьтің бойымен оң таңбамен алынған кесіндінің щамасы немесе абсолют мәні бағытталған кесіндінің ұзындығы делінеді. Кесіндінің абсолют мәні былайша белгіленеді: М1,М2, М2,М1. Мына М (х) нүктенің х координатасын ОМ-ніңабсолют мәні дейміз.

Теорема. М1, М2, М3 нүктелері остің бойына қандай болып тус­се де, ылғи мынадай теңдік орындалады:

М1М2 + M2M3 = М1М3. (2)

Дәлелдеу. х осінің бойында бұл үш нүкте мынадай алты жағдайда (4-сызба) болуы мүмкін: 1) М1 М2М3, 2) М1 М3 М2, 3) М2 М1 М3, 4) М2 М3 М1 5) М3 М1 М2, 6) М3 М2 М1

Бірінші жағдайда (4-сызба) М1М2, М2М3, М1М3 кесінділерінің ұзындықтары М1М2, М2М3, М1М3 кесінділеріңің ұзындықтарына тең. (2) тендіктің дұрыс екендігі төртінші сызбаның біріншісінен айқын көрінеді, өйткені М1М2, М2М3кесінділерінің қосындысы М1М3, кесіндісіне тең.

Екінші жағдайды біріншіге келтірейік:

М1М3 + М3М2 = М1М2

Осыдан М1М3 = М1М2 — М3М2. Ал М3М2 = - М2М3(өйткені M3M2мен М.2М3- тің таңбалары карама-қарсы). Сондықтан М1 М3 = М1М2 + М2М3

Қалған төрт жағдайларды осы сияқты дәлелдеуге болады. Осы теоремаға сүйеніп 4, 5, 6, ..., п нүктелері осьтің бойына қандай болып түссе де. мынадай теңдіктін дүрыс екендігін көрсету қиын емес:

МгМ2 + M2M3 + M3M4 + ...+ Мn-1 Мп = М1 Мп.

Теорема.Осінің, бойындағы бағытталған кесіндінің ұзындығын табу үшін кесіндінің соңғы нүктесінің координатасынан бірінші нүкіенің координатасын алу керек.

Дәлелдеу. Бізге х осінің бойында жатқан М1(х1), М2(х2) нүктелері берілсін (5-сызба). М1 М2 — бағытталған кесінді. 2 параграфтағы теорема бойынша осьтің бойындағы О, M1, M2 нүктелерінің 5-сызбадағы жағдайына сәйкес: ОМ1 + М1М2 = ОМ2. Осыдан М1М2 = ОМ2— ОМ1.

Теореманың шарты бойынша бізге берілгені: ОМ2 = х2, ОМ1= х1.

Табу керек: М1М2. Ал

М1 М2 = х2 —х1. (4)

Осыдан М1 М2 кесіндінің ұзындығы, яғни М1 (х1), М2 (х2) нүк-телерінің арасындағы қашықтық |М1 М2| кесіндісінің абсолют мәніне тең, яғни М1М2 = |М1 М2| = х2 — х1. Ал бағытталған кесіндінің (M1 М2) шамасын табу үшін ақырғы координата мен бастапқы координатаның айырымын алу керек. Сондықтан түзудің бойындағы кез келген екі нүктенің арасындағы кашықтык мынадай формуламен жазылады: М1 М2 = х2 — х1 немесе

d=x2 — х1. (5)

Түзудің бойындағы кесіндіні берілген қатынаста бөлу. Түзудің бойынан М1 (х1), М2(х2) нүктелері және

қатынасы берілсін. Осы (6) шартты қанағаттандыратын түзудің бойындағы М (х) нүктесін іздейік. 3-параграфтағы белгілеуіміз бойынша М1М, ММ2 кесінділерінің координаталарын (6) тендікке қоямыз:

 
 

Осыдан іздеген М(х) нүктесінің координатасын табамыз:

Бұл (8) тендік кесіндіні берілген катынаста бөлу формуласы деп аталады.

Егер λ =1 болса, онда (8) формула мынадай түрде жазылады:

(9)

Мүнда М нүктесі М1М2 кесіндісін қақ бөледі.

Егер λ = -1 болса, онда (8) теңдіктің бөлімі нольге тең. Бұл жағдайда мынадай түрде жазылады: λ = -1 санына ешбір М нүктесі сәйкес келмейді.

Жоғарыда жазылған

 

 

Жазықтықтағы нүктенің координаталары.Жазықтықта бір-біріне перпендикуляр болатын Охпен Oy остерін қарастырайық (6-сызба). Бұл осьтердің қилысатың О нүктесі екі оске жалпы координаталық бас нүкте болсын. Горизонталь Ox осін абсцисса осі деп, вертикаль О у осін ордината осі деп атайық. Абсцисса осінің оң бағытын О бас нүктесінен оңға қарай, ал ордината осінің оң бағытын О нүктесінен жоғары қарай алайық. Сонда осы екі оң бағыттардағы координаталардың таңбалары плюс ( + ), ал бүлбағыттарға қарама-қарсы координаталардың таңбалары минус ( — ) болады. Осы қиылысқан екі ось жазықтықты төртке (І, ІІ, ІІІ,ІV) бөледі (6-сызба).

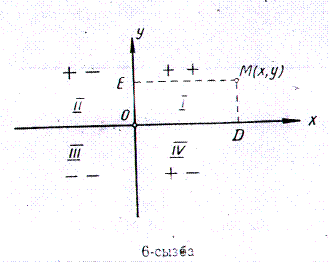Бірінші ширектегі нүкте координаталарының таңбалары ылғи плюс. Екінші ширектегі абсцис­са таңбасы минус, ординатаныкі плюс. Үшіншісінде екеуінікі де минус, төртіншісінде абсцисса таңбасы плюс, ординатаныкі минус.

Координаталар жазықтығынан бір М нүктесін алып, сол нүктеден осьтерге перпендикуляр түсірсек, онда М (х, у) нүктесінің координаталары x = OD, у —DM болады. х пен у сандары М нүктесінің координаталары деп аталады. Бұдан біз мынаны көреміз: жазыктықта бір нүкте берілсе, онда онын координатала­ры беріледі. Баскаша айтқанда, жазықтықтағы әрбір нүкте екі санмен (x = OD, y = DM) анықталады. Сөйтіп, жазыктыкта әрбір нүктеге екі сан сәйкес келеді, керісінше екі санға ылғи бір нүкте сәйкес болады.

Ох пен О у осьтерінің бойындағы кесінділерді өлшеу үшін әр түрлі масштаб (7-сызба), яғни абс­цисса осі үшін ml = OB1, ордината осі үшін m2= ОВ2 алуымыз керек. Басқаша айтқанда, әрбір осьтін бойынан еркімізше әр түрлі бірлік өлшеуіш алуға болады. Сонда М нүктесінің координаталары мынадай екі

 
 

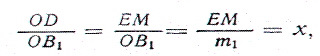тендік аркылы жазылады:

Абсцисса мен ордината осьтері координаталар осьтері деп ата­лады. В мен В2 нүктелерінің орнына Внүктесін алуға болады. Масштабы еркімізше алынған координаталар жүйесын аффиндік координаталар жүйесі деп атайды. Егер осы екі осьтің (Ох, Оу)бойындағы кесінділер бір масштабпен өлшенсе, яғни m1 = m2 = ОВ2 = ОВ1 = mболса, онда координаталар жүйесы декарттык, координаталар жүйесі деп аталады. Егер екі осьтін, (Ох, Оу) арасындағы бұрыш ω еркімізше (7-сызба) алынса, ондай жүйе қиғаш бурышты координаталар жүйесі деп аталады. Егер бұрыш ω = π/2 болса, ондай жүйе тік бұрышты немесе ортогональдық координаталар жүйесі деп аталады. Біз тік бұрышты декарттық координаталар жүйесін пайдаланамыз. Декарттык координаталар жүйесі болу үшін мынадай шарттар: 1) координаталардын, бас нүктесі, 2) осьтердің оң бағыттары, 3) ұзындықтың бірлік өлшеуіші (масштабы) берілу керек. Масштабты бірге тең (m = 1) деп алған қолайлы болады.

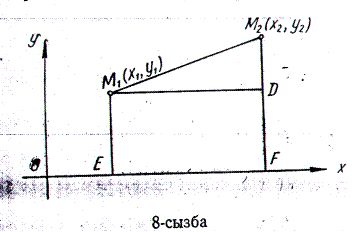Жазықтықтағы екі нүктенің ара қашықтығы. Жазықтықта М1(х1, у1), М2(х2, у2)екі нүктесі берілсін. Осы екі нүктенің ара қашықтығын табайық (8-сызба).

Берілген М1, М2 нүктелерінен абсцисса осіне М1Е және М2Ғ перпендикулярын түсірейік. Онан кейін М1 нүктесінен абсцисса осіне параллель M1 D сызығын жүргізсек, онда M1M2D тікбұрышты ұшбұрышы шығады. Осы тік бұрышты үшбұрыштан Пифагор Теоремасы бойынша (M1 D)2 + (DM2)2=(M1M2)2болады. Осы кесінділердің ұзындықтарын нүктелердің координаталары арқылы жазайық:

ОЕ = х2, ЕМ1 = у1, ҒМ2 = у2, EF= M1D = x2—-x1, DM2 = y2—y1.

Тік бұрышты үшбұрыштың M1D, DM2 катеттері мен М1М2 гипотенузасының орнына олардың координаталар арқылы шыққан мәндерін қойып, екі нүктенің ара қашықтығының формуласын табамыз:

 

Егер осы нүктелерді басқа ширектерден алсақ та, (11) формула өзгермейді, өйткені координаталардың айырымдары (х2—х1), (у2 – у1) қандай таңбалы сандар болса да, олардың квадраттары (х2—х1)2, (у2 – у1)2 ылғи оң таңбалы сандар болады.

Енді екі нүктенің біреуі, мысалы М1 (0,0) нүктесі, координаталардың бас нүктесінде жатсын. Осы жағдайда (11) формула мынандай түрге келеді:

(12)

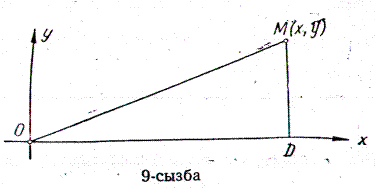Бұл — координаталардын бас нүктесінен жазықтықтағы берілген нүктеге дейінгі қашықтықтың формуласы (9-сызба). (12) фор­мула (11) формуланың дербес жағдайы: х1 = 0, у1 =0, х2=х, у2=у. Ал (12) формуланың дұрыс екендігі 9-сызбадан да айқын керінеді, яғни OD = x, DM = y, OM = d = x2+y2.

Жазықтықта О нүктесі мен одан шығатын Ох сәулесі берілсін. Жазықтықтағы кез-келген нүктеге М нүктесіне дейінгі арақашықтықты 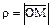– полярлық радиус арқылы, ал полярлық радиус пен Ох осі арасындағы бұрышты j – полярлық бұрыш арқылы белгілейік. Сонда жазықтықтағы кез-келген нүкте ρ, j шамалары арқылы бірмәнді анықталады. Осылайша анықталған жүйені жазықтықтағы полярлық координаталар жүйесі деп атаймыз. j – полярлық бұрыш, әрдайым сағат тіліне қарсы бұру арқылы анықталады. Егер полярлық бұрыш сағат тілімен бағыттас бұру арқылы анықталса, онда оған *-* таңбасы қойылады.

Полярлық бұрыш 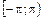немесе 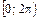аралығында өзгереді.

М(ρ, j) нүктесі полярлық координаталар арқылы берілсін. М нүктесінің декарттық координаталарын анықтайық. Суретте көрсетілген тік бұрышты үшбұрыштан:

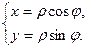(13)

екендігі шығады. (13) полярлық координатадан декарттық координатаға көшу формуласы деп аталады.

Егер М(х,у) нүктесі декарттық координаталар арқылы берілсе, онда М нүктесінің полярлық координаталары:

(14)

(14) -декарттық координаталардан полярлық координаталарға көшу формуласы деп аталады.