Векторами прямой то векторы называются ортогональными.

Определение: Ортогональной проекцией

вектора 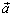на

направление вектора

называется скалярная величина

, φ – угол между векторами (рис.9).

Модуль этой скалярной величины равен длине отрезка OA₀.

Если угол φ острый проекция является положительной величиной, если угол

φ тупой – проекция отрицательна, если угол φ прямой – проекция

Равна нулю.

При ортогональной проекции угол между отрезками OA₀ и AA

₀ прямой. Существуют проекции, у которых этот угол отличен от прямого.

Проекции векторов обладают следующими свойствами:

1. (проекция суммы равна сумме проекций);

2. (проекция

Произведения вектора на число равна произведению проекции вектора на число).