Называют «правилом треугольника».

Операция сложения векторов обладает свойствами:

1. (коммутативность);

2. , (ассоциативность);

3. 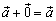для любого вектора 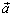(особая роль нулевого вектора);

4. для каждого вектора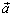

существует противоположный ему вектор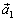

такой, что (для получения

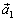
достаточно поменять местами начало и конец вектора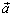

).

Вектор противоположный вектору 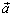обозначают .

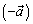Определение: Разностью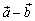

векторов 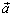и

называется сумма вектора 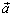и

вектора противоположного вектору

, т.е.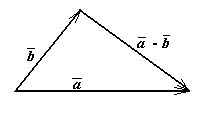

.

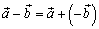
Разность 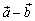получается из вектора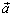

сдвигом его начала в конец вектора

, при условии, что векторы 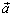и

имеют общее начало (рис.3). Очевидно, что

для любого вектора 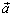.