Построение кривой разгона
Кривой разгона называют процесс изменения во времени выходной переменной, вызванный ступенчатым входным воздействием. Кривая разгона служит для определения динамических свойств объекта.
Запаздывание объекта выражается в том, что его выходная величина начинает изменяться не сразу после нанесения возмущения, а только через некоторый промежуток времени, называемым временем запаздывания.
Под постоянной времени объекта понимается время, в течение которого выходная величина достигла бы своего нового установившегося значения, если бы она изменялась с постоянной скоростью, равной скорости ее изменения в начальный момент времени.
Коэффициент передачи объекта представляет собой изменение выходной величины объекта при переходе из начального в новое установившееся состояние, отнесенное к изменению возмущения на входе [1].
Снятие кривой разгона предусматривает нанесение на объект ступенчатого возмущения путем энергичного изменения степени открытия проходного сечения регулирующего органа, при этом отмечают величину и момент нанесения возмущения. Изменения выходной величины регистрируют до тех пор, пока объект не примет установившееся значение.
Кривая разгона отличается от переходной характеристики тем, что амплитуда «скачка» может быть произвольной, в то время как переходная характеристика есть реакция объекта управления на единичный скачок по управляющей переменной [2].
Кривая разгона получается пересчетом безразмерной кривой разгона по формулам
t = Mt . tб
Δy = My . Δyб
где t – реальное время,
tб – безразмерное время,
Mt – масштаб времени,
My – масштаб регулируемой переменной,
Δy – изменение регулируемой переменной в натуральных единицах,
Δyб – изменение регулируемой переменной в безразмерном виде
Рассчитаем кривую разгона (таблица 2)
Таблица 2 – Пересчитанная кривая разгона
| t, мин | 2,4 | 4,8 | 7,2 | 9,6 | 14,4 | ||
| Δy, мм.в.ст. | 0,043 | 0,301 | 1,075 | 1,849 | 2,494 | 3,01 | |
| t, мин | 16,8 | 19,2 | 21,6 | 26,4 | 28,8 | 31,2 | |
| Δy, мм.в.ст. | 3,354 | 3,612 | 3,784 | 3,913 | 4,042 | 1,128 | 4,171 |
| t, мин | 33,6 | 38,4 | 40,8 | 43,2 | 45,6 | ||
| Δy, мм.в.ст. | 4,214 | 4,2355 | 4,257 | 4,3 | 4,3 | 4,3 |
Кривая разгона представлена на рисунке 1.
Определим параметры аппроксимации кривой разгона. Касательная касается кривой разгона в точке А1, соответствующей максимальной крутизне.
В соответствии с рисунком 1 коэффициент передачи равен
Коб = Δyуст / ΔU
Коб = 4,3 / 8 = 0,54 мм.в.ст./%
где Δyуст – установившееся значение выходной переменной,
ΔU – изменение входной переменной.
Передаточная функция данной аппроксимации будет иметь вид
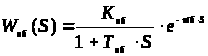
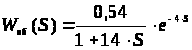
где Коб – коэффициент передачи объекта,
Тоб – постоянная времени (Тоб = 18 – 4 = 14 мин),
τоб – время запаздывания, (τоб = 4 мин),
S – переменная Лапласа.










Кривой разгона звена называется зависимость выходной величины хВЫХ от времени (хВЫХ = f(t)) при скачкообразном изменении входной величины хВХ. При этом входная величина после скачкообразного изменения остаётся постоянной.
Кривая разгона (кривая переходного процесса) является одной из основных динамических характеристик звена.
Несмотря на различие объектов, кривые их разгона могут быть отнесены к нескольким характерным группам: кривые разгона апериодического, колебательного, интегрирующего звеньев и т.д. Из кривой разгона графически или графоаналитически определяются основные параметры звена.
В инженерной практике широко используется экспериментальный способ определения кривой переходного процесса (кривой разгона) при воздействии на вход объекта (элемента системы) единичного скачка или единичного импульса (снятие импульсной переходной функции или функции веса). В последующем указанные кривые переходного процесса аппроксимируются дифференциальными уравнениями.
Одним из методов получения дифференциального уравнения по кривой разгона, который можно порекомендовать студентам, является метод А. Н. Крылова, данный метод [7, с. 113-115] используется, если есть основания предположить, что кривая разгона может быть аппроксимирована дифференциальным уравнением второго порядка.
Более универсальным является метод площадей, хотя он требует большего объема вычислительной работы. Подробнее изложение указанного метода и примеры его применения можно найти в учебных пособиях [15, с. 60-67], [17, задачи 1.64, 1.69], а также [16, 19]. Для оценочных расчетов можно использовать упрощенные методы определения дифференциальных уравнений и их коэффициентов, изложенные в учебных пособиях [18, с. 8-23], [9, с. 235-245]. Во всех случаях аппроксимации кривой разгона дифференциальным уравнением представляется целесообразным построение переходного процесса по полученному дифференциальному уравнению, сопоставление его с исходной кривой разгона и оценки точности аппроксимации.























































12. Законы регулирования. Импульсные и непрерывные регуляторы
| ТИПОВЫЕ ЗАКОНЫ РЕГУЛИРОВАНИЯ И ИХ РЕАЛИЗАЦИЯ | |
| В системах автоматического регулирования поддержание заданного значения регулируемого параметра или изменение его по определенному закону обеспечивается аппаратурными средствами, имеющие общее название – автоматические регуляторы. По виду регулируемого параметра автоматические регуляторы подразделяются на регуляторы температуры, давления, влажности, разряжения, расхода, состава и т. п. По характеру изменения регулирующего воздействия автоматические регуляторы подразделяются на регуляторы с линейными и нелинейными законами регулирования. Примером регуляторов с нелинейным законом регулирования могут служить двухпозиционные регуляторы температуры в холодильных машинах. В трехпозиционных дискретных системах выходной сигнал может принимать три значения: –1, 0, +1, т.е. “меньше”, “норма”, больше”. Качество работы таких САР выше, хотя их надежность ниже. Регуляторы с линейным законом регулирования по математической зависимости между входными и выходными сигналами подразделяются на следующие основные виды: · пропорциональные (П-регуляторы); · пропорционально-интегральные (ПИ-регуляторы); · пропорционально-интегрально-дифференциальные (ПИД-регуляторы). В зависимости от вида используемой энергии регуляторы подразделяются на электрические (электромеханические, электронные), пневматические, гидравлические и комбинированные. Пневматические и гидравлические регуляторы, как правило, применяются во взрыво- и пожароопасных зонах. В зависимости от задающего воздействия и параметров объекта регулирования подбирают регулятор с определенной характеристикой Wр . Изменение Wр адекватно ведет к изменению коэффициентов дифференциального уравнения общего передаточного звена (регулятор-объект) и тем самым достигается необходимое качество регулирования. В промышленных регуляторах эти величины называются параметрами настройки. Параметрами настройки являются: коэффициент усиления, зона нечувствительности, постоянная времени интегрирования, постоянная времени дифференцирования и т. д. Для изменения параметров настройки в регуляторах имеются органы настройки (управления). Кроме органов настройки основных параметров, регуляторы имеют также органы настройки, косвенно влияющие на эти коэффициенты или режимы его работы, например, органы настройки, изменяющие чувствительность регулятора, демпфирование входного сигнала и др. | |
| Пропорциональные регуляторы Обобщенная структурная схема САР представлена на рис. 1. | |

| 
|
| а | б |
| Рис. 1 Структурная схема САР: а – разомкнутой системы по каналу задающего воздействия; б – то же, но замкнутой системы | |
| Для системы регулирования, показанной на рис. 1, ее амплитудно-фазовая характеристика (АФХ) определяется выражением W(jω) = Wp(jω) · Wоб(jω), (1.1) где Wp(jω) – АФХ регулятора; Wоб(jω) – АФХ объекта регулирования. Если комплексная частотная характеристика регулятора будет Wp(jω) = kp, (1.2) то АФХ всей системы запишется в виде W (jω) = kp · Wоб(jω). (1.3) Следовательно, при подключении к объекту регулятора с АФХ (1.2) АФХ системы на каждой частоте увеличивается в kp раз. Такие регуляторы называются пропорциональными (П-регуляторы) и имеют один параметр настройки – коэффициент передачи kp. Переходные процессы в П-регуляторе описываются выражением μ = kp · ε, (1.4) где ε – входное воздействие на регулятор, равное отклонению регулируемой величины от заданного значения; μ – воздействие регулятора на объект, направленное на ликвидацию отклонения регулируемой величины от заданного значения. На рис. 2 приведен пример контура регулирования температуры приточного воздуха в канальном кондиционере. Температура воздуха поддерживается водяным калорифером, через который пропускается теплоноситель. Воздух, проходя через калорифер, нагревается. Температура воздуха после водяного калорифера измеряется датчиком (Т), далее эта величина поступает на устройство сравнения (УС) измеренного значения температуры (Тизм) и заданного (Tзад). В зависимости от разности между температурой уставки и измеренным значением температуры регулятор (Р) вырабатывает сигнал, воздействующий на исполнительный механизм (М – электропривод трехходового клапана). Электропривод открывает или закрывает трехходовой клапан до положения, при котором ошибка ε = Tзад – Тизм будет стремиться к нулю. Выходным сигналом регулятора может быть напряжение в определенном диапазоне (например, постоянное напряжение в диапазоне от 0 до 10 В, ток 0–20мА и т. д). Диапазон изменения выходного сигнала называется диапазоном регулирования (рис.3). Диапазон изменения сигнала ошибки называют пропорциональным диапазоном. В П-регуляторах имеется возможность изменять диапазон регулирования и пропорциональный диапазон. | |

| 
|
| Рис.3 Контур регулирования температуры приточного воздуха в канале центрального кондиционера | Рис.4 График пропорционального регулирования |
Из графика (рис.4) видно, что чем меньше пропорциональный диапазон, тем круче характеристика регулирования. Кривая (1) соответствует диапазону изменения температуры 0–10 °С, а кривая (2) – диапазону 0–4°С. Величина kp =  есть коэффициент регулирования. В первом случае kp = 1, а во втором kp = 2,5. При больших значениях kp в контуре регулирования могут возникнуть колебания (рис.5). Так, если во время включения системы температура воздуха Тизм ниже заданной температуры Tзад, устройство управления выдает большой сигнал на открытие трехходового клапана. Температура водяного калорифера и приточного воздуха начнет повышаться. Когда температура приточного воздуха после водяного калорифера достигает Tзад, устройство управления выдает команду на закрытие трехходового клапана (точка t1, рис. 5). Однако из-за того, что калорифер разогрет, температура приточного воздуха до момента t2 еще будет расти, а затем начнет снижаться. Этот процесс имеет вид затухающих колебаний, и через определенное время (t3) процесс стабилизируется. После стабилизации из-за инерционности системы всегда будет существовать статическая ошибка Δст = Tзад – Тизм. Сигнал на выходе устройства управления будет иметь вид y(t) = U0 + kp · ε, (1.5) где U0 – сигнал на выходе устройства управления при ε = 0. есть коэффициент регулирования. В первом случае kp = 1, а во втором kp = 2,5. При больших значениях kp в контуре регулирования могут возникнуть колебания (рис.5). Так, если во время включения системы температура воздуха Тизм ниже заданной температуры Tзад, устройство управления выдает большой сигнал на открытие трехходового клапана. Температура водяного калорифера и приточного воздуха начнет повышаться. Когда температура приточного воздуха после водяного калорифера достигает Tзад, устройство управления выдает команду на закрытие трехходового клапана (точка t1, рис. 5). Однако из-за того, что калорифер разогрет, температура приточного воздуха до момента t2 еще будет расти, а затем начнет снижаться. Этот процесс имеет вид затухающих колебаний, и через определенное время (t3) процесс стабилизируется. После стабилизации из-за инерционности системы всегда будет существовать статическая ошибка Δст = Tзад – Тизм. Сигнал на выходе устройства управления будет иметь вид y(t) = U0 + kp · ε, (1.5) где U0 – сигнал на выходе устройства управления при ε = 0.
| |

| |
| Рис.5 Переходной процесс при пропорциональном (П) регулировании | |
| Чем большим выбран пропорциональный диапазон регулирования, тем большей будет величина статистической ошибки. При малой величине пропорционального диапазона увеличивается время переходных процессов, и при некоторых условиях может возникнуть автоколебательный (незатухающий) процесс в контуре регулирования. Путем выбора параметров регулирования П-регулятора можно существенно уменьшить установившуюся ошибку регулирования, однако ее полное устранение непредставляется возможным даже теоретически. Из рис.3 видно, что в цепочке регулирования в реальном регуляторе установлено еще одно звено – исполнительный механизм (М). В данном случае – это электродвигатель привода трехходового клапана. Электрический привод является интегрирующим звеном иего влияние по возможности уменьшают, используя обратные связи. Это связано с тем, что динамические свойства участка, охваченного обратной связью, независят от динамических свойств прямого участка, а определяются в основном динамическими свойствами звена обратной связи. Эта особенность широко используется напрактике при разработке автоматических регуляторов. Исходя из этого, для устранения влияния исполнительного механизма его необходимо охватить отрицательной обратной связью. Для повышения коэффициента передачи прямого канала отрицательной обратной связью нужно охватить и усилительное звено регулятора. Такие П-регуляторы, называемые позиционерами, можно представить в виде последовательного соединения собственно П-регулятора и некоторого балластного звена с постоянной времени Тб. На рис. 6 представлена структурная схема П-регулятора, а на рис. 7 – реализуемый ею закон регулирования. | |

| 
|
| Рис.6 Структурная схема П-регулятора | Рис.7 Закон П-регулирования |
| Параметром настройки регулятора является коэффициент передачи устройства обратной связи kос. Коэффициент передачи регулятора kп тем больше, чем меньше kос. Однако следует иметь в виду, что чем больше kп, тем больше постоянная времени балластного звена и тем больше искажается идеальный закон П-регулирования. | |
| Пропорционально-интегральные регуляторы | |
Статическую ошибку, возникающую при пропорциональном регулировании, можно исключить, если кроме пропорционального ввести еще и интегральное звено. Последнее образуется путем постоянного суммирования ε за определенный промежуток времени иформирования сигнала управления, пропорционального полученной величине. Математически этот процесс может быть описан следующей зависимостью:  , (1.6) где kи=1/Ти – коэффициент пропорциональности интегральной составляющей, а Ти - постоянная времени интегрирования, параметр настройки регулятора. Если kи ≠ 0, то даже при незначительных отклонениях регулируемой величины сигнал со временем может достичь любой величины, что приведет к перемещению регулирующего органа до момента, пока ε не станет равным 0. Рассмотрим физический смысл постоянной времени интегрирования. Предположим, что на вход регулятора поступил сигнал ε = ε 0, а пропорциональная составляющая отсутствует (kп = 0). При этом выходной сигнал в соответствии (1.6) будет меняться по закону μ = ε0 · t/Tи. По истечении времени t = Tи значение выходного сигнала будет равно μ = ε0 (рис.8, а). Таким образом, постоянная времени интегрирования в И-регуляторе равна времени, в течение которого с момента поступления на вход регулятора постоянного сигнала сигнал на выходе регулятора достигнет значения, равного значению входного сигнала. Переходной процесс в И-регуляторе показан на рис.8, б. Устраняя статическую ошибку интегральный регулятор, однако, ухудшает качество переходного процесса. Поэтому на практике применяют комбинированные ПИ-регуляторы. , (1.6) где kи=1/Ти – коэффициент пропорциональности интегральной составляющей, а Ти - постоянная времени интегрирования, параметр настройки регулятора. Если kи ≠ 0, то даже при незначительных отклонениях регулируемой величины сигнал со временем может достичь любой величины, что приведет к перемещению регулирующего органа до момента, пока ε не станет равным 0. Рассмотрим физический смысл постоянной времени интегрирования. Предположим, что на вход регулятора поступил сигнал ε = ε 0, а пропорциональная составляющая отсутствует (kп = 0). При этом выходной сигнал в соответствии (1.6) будет меняться по закону μ = ε0 · t/Tи. По истечении времени t = Tи значение выходного сигнала будет равно μ = ε0 (рис.8, а). Таким образом, постоянная времени интегрирования в И-регуляторе равна времени, в течение которого с момента поступления на вход регулятора постоянного сигнала сигнал на выходе регулятора достигнет значения, равного значению входного сигнала. Переходной процесс в И-регуляторе показан на рис.8, б. Устраняя статическую ошибку интегральный регулятор, однако, ухудшает качество переходного процесса. Поэтому на практике применяют комбинированные ПИ-регуляторы.
| |

| 
|
| Рис.8 Закон регулирования (а) и переходной процесс (б) при интегральном (И) регулировании | |
При этом используется как параллельное соединение пропорционального и интегрального звена (рис.8, а), так и последовательного (рис.8, б). ПИ-регулятор оказывает воздействие на регулирующий орган пропорционально отклонению и интегралу от отклонения регулируемой величины.  (1.7) Передаточная функция ПИ-регулятора (по схеме, рис.8, а): Wпи(р) = kp+ (1.7) Передаточная функция ПИ-регулятора (по схеме, рис.8, а): Wпи(р) = kp+  (1.8) (1.8)
| |

| 
|
| Рис.9. Структурная схема идеальныхПИ-регуляторов: а – с передаточной функцией (1.8);б – с передаточной функцией (1.10) | Рис.10. Закон ПИ-регулирования регуляторов 1 – спередаточной функцией (1.8) 2 – с передаточной функцией (1.10) |
При скачкообразном изменении регулируемой величины на значение ε0 ПИ-регулятор со скоростью, определяемой быстродействием привода, перемещает исполнительный механизм на величину (kp · ε0), после чего исполнительный механизм дополнительно перемещается в ту же сторону со скоростью ε0/Ти, пропорциональной отклонению регулируемой величины. Следовательно, в ПИ-регуляторе при отклонении регулируемой величины от заданного значения мгновенно срабатывает пропорциональная (статическая) составляющая регулятора, а затем постепенно увеличивается интегральная (астатическая) составляющая регулятора. Переходная характеристика ПИ-регулятора с передаточной функцией (1.8) показана на рис.10 (прямая 1). Параметрами настойки являются независящие друг от друга коэффициенты усиления kp и постоянная времени интегрирования Ти. Схема на рис.9, б реализует закон регулирования  (1.9) где Тиз – постоянная времени изодрома. Передаточная функция ПИ-регулятора по схеме рис.9,б: Wпи(р) = (1.9) где Тиз – постоянная времени изодрома. Передаточная функция ПИ-регулятора по схеме рис.9,б: Wпи(р) =  (1.10) Таким образом, ПИ-регулятор со структурной схемой, приведенной на рис.9, б, имеет взаимосвязанные параметры настройки статической и астатической частей по коэффициенту kp. Так, при настройке коэффициента усиления kp будет изменяться и постоянная времени интегрирования: (1.10) Таким образом, ПИ-регулятор со структурной схемой, приведенной на рис.9, б, имеет взаимосвязанные параметры настройки статической и астатической частей по коэффициенту kp. Так, при настройке коэффициента усиления kp будет изменяться и постоянная времени интегрирования:  (1.11) Рассмотрим физический смысл постоянной времени изодрома Тиз. Предположим, что на вход регулятора поступил постоянный сигнал ε0. Тогда выражение (1.9) преобразуется к виду μ = kp ε0(1+t/T) (1.12) (1.11) Рассмотрим физический смысл постоянной времени изодрома Тиз. Предположим, что на вход регулятора поступил постоянный сигнал ε0. Тогда выражение (1.9) преобразуется к виду μ = kp ε0(1+t/T) (1.12)
| |

| |
| Рис.11. Переходной процесс при пропорционально-интегральном (ПИ) регулировании | |
| При поступлении на вход регулятора сигнала ε0 в начальный момент сработает пропорциональная составляющая и на выходе регулятора появится сигнал μ1=kpε0. В дальнейшем по закону (1.12) линейно начинает нарастать выходной сигнал от интегральной составляющей и при t= Tиз достигнет значения μ2=2kpε0. Таким образом, Тиз – это время, в течение которого от начала действия интегральной (астатической) составляющей регулятора пропорциональная (статическая) составляющая удваивается. Переходной процесс при ПИ-регулировании показан на рис.11. Варианты структурных схем ПИ-регуляторов приведены на рис.12. | |

| 
|
| а | б |

| 
|
| в | г |
| Рис.12. Структурные схемы промышленных ПИ-регуляторов | |
Пропорционально-интегрально-дифференциальные (ПИД) регуляторы П- и ПИ-регуляторы не могут упреждать ожидаемое отклонение регулируемой величины, реагируя только на уже имеющееся отклонение. Возникает необходимость в регуляторе, который вырабатывал бы дополнительное регулирующее воздействие, пропорциональное скорости отклонения регулируемой величины от заданного значения  (1.13) Такое регулирующее воздействие используется в дифференциальных и ПИД-регуляторах. ПИД-регуляторы воздействуют на объект пропорционально отклонению ε регулируемой величины, интегралу от этого отклонения и скорости изменения регулируемой величины: (1.13) Такое регулирующее воздействие используется в дифференциальных и ПИД-регуляторах. ПИД-регуляторы воздействуют на объект пропорционально отклонению ε регулируемой величины, интегралу от этого отклонения и скорости изменения регулируемой величины:  (1.14) По возможностям ПИД-регуляторы являются универсальными. Используя их, можно получить любой закон регулирования. Структурная схема и закон регулирования идеального ПИД-регулятора приведены на рис.13 (1.14) По возможностям ПИД-регуляторы являются универсальными. Используя их, можно получить любой закон регулирования. Структурная схема и закон регулирования идеального ПИД-регулятора приведены на рис.13
| |

| 
|
| а | б |
| Рис.13. Cтруктурная схема ПИД-регулятора (а) и закон ПИД-регулирования (б) | |
| При скачкообразном изменении регулируемой величины ПИД-регулятор в начальный момент времени оказывает мгновенное бесконечно большое воздействие на объект регулирования, затем величина воздействия резко падает до значения, определяемого пропорциональной составляющей, после чего постепенно начинает оказывать влияние интегральная составляющая регулятора. Переходной процесс при этом (рис.14) имеет минимальные отклонения по амплитуде и по времени. Параметрами настройки ПИД-регуляторов являются коэффициент пропорциональности регулятора kp, постоянная времени интегрирования Ти и постоянная времени дифференцирования Тд. | |

| |
| Рис.14 Переходной процесс при ПИД- регулировании |


























































































