Медиана

Медиана в статистике – это значение признака в возрастающем или убывающем вариационном ряду, которое находится в середине ряда.

Медиана делит все единицы совокупности на две части, со значениями признака выше и ниже медианы.

 

Для нахождения медианы в дискретном ряду необходимо ранжировать ряд (выстроить его в порядке возрастания), а затем определить «позицию» медианы или определить номер той единицы, значение признака у которой будет соответствовать медиане:

N_Ме= ,

где n – число единиц в исследуемой совокупности.

Если ранжированный ряд включает в себя четное число единиц, то медиана определяется как средняя из двух центральных значений.

 

Построим ранжированный ряд распределения числа деталей.

№	Х1	Х2	Х3	Х4	Х5	Х6	Х7	Х8	Х9
Число деталей					10

N_Ме= , то есть медиана равна средней арифметической из 6 и 7 значения признака.

Ме = 10 деталей

 

Для нахождения медианы в интервальном ряду, вначале определяют медианный интервал. Он определяется номером медианы N_Ме= .

Нахождение медианы осуществляется по формуле:

Ме = ,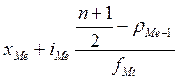

где х_Ме – нижняя граница медианного интервала

i_Mе – величина медианного интервала

r_Mе-1 – накопленная частота интервала предшествующего медианному

f_Mе – частота последующая медианному интервалу

 

По данным примера распределения групп заводов по стоимости основных фондов, используя накопленные частоты, медиана находится в интервале 34 – 36. Тогда:

Ме = 35,2 млрд. руб.

Таким образом, 50% предприятий имеют основные фонды до 35,2 млрд. руб., а 50% более 35,2 млрд. руб.