Синтез эквивалентных схем фильтров

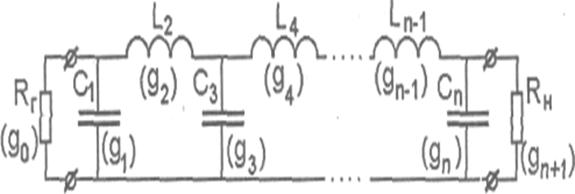
Рассмотрим синтез эквивалентной схемы ФНЧ, выполненной по лестничной схеме. Такая схема, состоящая из п элементов L и С, показана на рис. 14.23. Внутреннее сопротивление R_r генератора, подключенного к входу схемы, и сопротивление R_H нагрузки на ее выходе считаем активными и равными друг другу. Отметим, что во многих практических приложениях главное значение имеет АЧХ фильтра, в то время как другие характеристики (фазочастотная характеристика, характеристика группового времени задержки и др.) обычно рассматриваются и при необходимости корректируются после

Рис. 14.23

 

получения желаемой АЧХ фильтра. Ниже рассматривается синтез эквивалентных схем фильтров по заданной АЧХ. Идеальную АЧХ для ФНЧ (рис.14.22,а) невозможно получить с помощью схемы, имеющей конечное число элементов n. Поэтому обычно используют более приемлемый для практики способ задания требований к АЧХ: в диапазоне частот 0<f<f_c (полоса пропускания) величина вносимого затухания не должна превышать заданную величину В_Ф1, а в полосе f₃<f<¥ (полоса заграждения) вносимое затухание должно быть больше заданной величины В_Ф2 (рис.14.24). Указанную идеализированную АЧХ аппроксимируют той или иной функцией.

Наибольшее распространение на практике получили два вида аппроксимации: максимально плоская и чебышевская.

В первом случае вносимое затухание для n-звенного фильтра описывается функцией, предложенной Баттервортом [35]:

(14.5)

где h = 10^Вф1/10-1, а для ФНЧ W= f/f_c. Зависимость B_ф от f при разных n показана на рис. 14.25, а. Как следует из рисунка, при f«f_c В_ф@0 и не зависит от частоты. Подобная АЧХ максимально приближена к идеальной АЧХ в полосе пропускания, отсюда и ее название - максимально плоская АЧХ. При фиксированных величинах fс, B_Ф1 и fз увеличение числа элементов в схеме n приводит к возрастанию

Рис. 14.25

 

величины В_Ф2 (см. рис.14.25,а) или при фиксированных величинах f_c, В_Ф1 и В_ф2-к уменьшению разницы между f₃ и fс, т.е. увеличивается крутизна АЧХ.

Во втором случае АЧХ фильтра аппроксимируется с помощью полиномов Чебышева [35]:

(14.6)

где Т_n(х)-полином Чебышева первого рода порядка п, описываемый выражениями

Tn(x) =

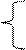cos[n arccos(x)] при 0£|х|£1,

ch[n arch(x)] при |х|>1.

Типичная чебышевская АЧХ фильтра нижних частот показана при разных п на рис. 14.25, б. В полосе пропускания подобная АЧХ имеет осциллирующий характер с неизменной амплитудой осцил­ляции. Увеличить крутизну АЧХ при неизменной амплитуде ос­цилляции можно, лишь используя схему, с большим числом эле­ментов п. Основное преимущество чебышевских фильтров по сравнению с максимально плоскими-меньшее число элементов в схеме при одинаковых значениях В_Ф1, В_Ф2, fc и fз.

Отметим, что при передаче через фильтр электромагнитных сигналов с достаточно широким спектром частот (широкополосные сигналы) важное значение имеет вид фазочастотной характеристики (ФЧХ) фильтра; ФЧХ-это зависимость аргумента j₂₁ коэффициента передачи фильтра S₂₁=|S₂₁|exp(ij₂₁) от частоты. Предполагается, что у идеального фильтра ФЧХ является ли­нейной функцией частоты. При этом широкополосный сигнал проходит через такой фильтр без искажений.

При одинаковых исходных данных ФЧХ максимально плоского фильтра более близка к линейной, чем аналогичная характеристика чебышевского фильтра.

Из (14.5) и (14.6) можно получить следующие формулы для определения числа звеньев в схеме фильтра: для максимально плоского фильтра

(4.7)

для чебышевского фильтра

 

(14.8)

где для ФНЧ Q₃ = f₃/f_c. Обычно при вычислениях по (14.8) используют тождество

arch (x) = ln (x + Öx²-1).

 

На практике, как правило, синтез эквивалентных схем фи­льтров разных типов проводят с помощью синтеза схемы фильтра-прототипа нижних частот. Схема такого фильтра совпадает со схемой ФНЧ (рис.14.23) и имеет такое же число звеньев, а параметры его элементов обозначаются буквами g₁, g₂,.. g_n (g₀ и g_n+1 соответствуют активным сопротивлениям генератора и наг­рузки). Эти параметры (иногда их называют g-параметрами) явля­ются нормированными параметрами элементов ФНЧ, так как они равны параметрам элементов ФНЧ при

w_с = 1 рад/с и R_H=R_r=1 Ом.

Для фильтра-прототипа g-параметры определяют по следующим формулам [34]:

для максимально плоского фильтра

g₀ = g_n+1=1, j= 1,2 ..... п, (14.9)

 

для чебышевского фильтра

g_o = 1, g₁= 2a₁/y, g _j =4a _{j – 1} a_j / (b _{j -1} g _{j - 1}), j=2, 3, ...,п; (14.10)

gn+1=

1 при нечетном п,

cth²(p/4) при четном n;

где a _j = sin[(2j-1)p/(2n)], b_j = y² + sin²(jn/n), y = sh [p/(2n)],

p= ln[сth(В_{ф 1}/17,37)].

Отметим, что для максимально плоских фильтров элементы с одинаковыми значениями g в схеме (рис.14.23) расположены сим­метрично относительно середины фильтра как для четных, так и для нечетных значений п. Поэтому к входу и выходу фильтра

 

Рис. 14.26

должны подключаться одинаковые сопротивления go=g_n+1._`

Для чебышевских фильтров указанное свойство выполняется лишь для нечетного числа звеньев в схеме, при п четном симметрия нарушается и получается g₀¹g_n+1. При необходимости подключения одинаковых сопротивлений к входу и выходу чебышевского фильтра с четным числом звеньев (например, если фильтр встраивается в линию передачи с заданным волновым сопротивлением) следует включить в схему такого фильтра дополнительный трансформатор сопротивлений.

Исходными данными при синтезе эквивалентной схемы ФНЧ являются следующие величины (рис. 14.24): f_С, f_З, B_ф1, B_ф2, R_H и вид АЧХ. Вначале с помощью исходных данных вычисляют по (14.7) или (14.8) число звеньев в эквивалентной схеме фильтра. Затем по формулам (14.9) или (14.10) рассчитывают g-параметры элементов схемы фильтра - прототипа. Для получения формул, связывающих величины индуктивностей и емкостей эквивалентной схемы ФНЧ с g-параметрами, приравняем нормированные проводимости (умноженные на R_H) элементов, образующих параллельные ветви схемы, и нормированные сопротивления (деленные на rh) элементов, образующих последовательные ветви схемы, проводимостям и сопротивлениям соответствующих элементов фильтра-прототипа:

(14.11)

где j=1,2, ...,т; т=п/2 при n четном и m = (n + 1)/2 при п нечетном.

С учетом того, что для ФНЧ Q = f/f_c, из (14.1 1) получим

(14.12)

Рассмотрим синтез эквивалентной схемы ПФ, выполненной по лестничной схеме. Такая схема, состоящая из п последовательных и параллельных контуров из L и С, изображена на рис. 14.26. И в этом случае при синтезе эквивалентной схемы используют идеализированную АЧХ (рис. 14.27),

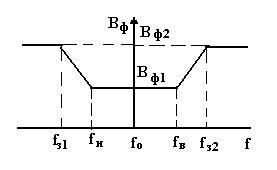
Рис. 14. 27

Рис. 14.28

для которой в полосе пропускания фильтра f_H£f£f_Bвносимое затухание В_ф£В_ф1, а в полосе заграждения f£f₃₁ и f³f₃₂ вносимое затухание В_ф³В_ф2. Для максимально плоской аппроксимации этой АЧХ используется функция (14.5), а для чебышевской- функция (14.6), в которой необходима следующая замена частотной пере­менной:

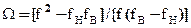(14.13)

Следует отметить, что при замене (14.13) АЧХ фильтра-прототипа переходит в АЧХ полосового фильтра (на рис. 14.28 показано преобразование максимально плоской АЧХ).

Исходными данными при синтезе эквивалентной схемы ПФ (см. рис.14.27) являются следующие величины: f_H, f_B, f₃₁, f₃₂, В_Ф1, В_Ф2, R_H и вид АЧХ. Вначале с помощью исходных данных вычи­сляют по (14.7) или (14.8) при общее число контуров n в эквивалентной схеме фильтра, равное числу элементов в схеме фильтра-прототипа. Затем по формулам (14.9) или (14.10) рассчитывают g-параметры элементов схемы фильтра-прототипа. Действуя как и в случае синтеза эквивалентной схемы ФНЧ, несложно получить следующие формулы для расчета параметров элементов контуров эквивалентной схемы ПФ через g-параметры фильтра-прототипа:

в случае параллельных контуров

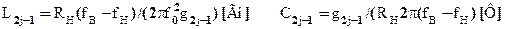(14.14)

а для последовательных контуров

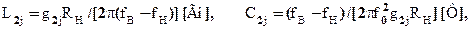(14.15)

где j=1,2 …,т; т=п/2 при четном n и m = (n + 1)/2 при нечетном n;

Нагруженная добротность контуров эквивалентной схемы ПФ определяется по формуле [35]:

(14.16)

Аналогичным образом, используя результаты синтеза фильтра-прототипа и выбирая соответствующую замену частотной пе­ременной в аппроксимирующей функции для АЧХ, синтезируются эквивалентные схемы фильтров верхних частот и режекторные фильтры [35].

Рассмотрим еще одну эквивалентную схему фильтров, выполненную по лестничной схеме. Если в формулах (14.5) или (14.6), аппроксимирующих АЧХ фильтра прототипа (рис.14.23), использовать следующую замену частотной пере­менной где l-длина отрезка линии передачи, по которой распространяется волна с фазовой скоростью J_ф, АЧХ фильтра-прототипа пере­ходит в АЧХ, имеющую вид периодической функции частоты (на рис.14.29 показано подобное преобразование для максимально плоской АЧХ). При подобной замене частотной переменной реактивное сопротивление любого индуктивного элемента в схеме фильтра-прототипа (см. рис.14.23) переходит во входное реактивное сопро­тивление короткозамкнутого шлейфа длиной l (12.28),

т.е.

-волновое сопротивление шлейфа. Аналогично реак­тивная проводимость любого емкостного элемента в схеме рис.14.23 переходит во входную реактивную проводимость разомкнутого шлейфа длиной l (см. формулу (12.28)),

т.е

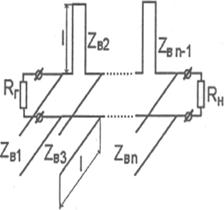
-волновое сопротивление шлейфа. Значит, схема фильтра-прототипа рис.14.23 переходит в схему рис.14.30, образованную последовательно и параллельно подключенными короткозамкнутыми и разомкнутыми реактивными шлейфами.

Рис.14.29

Рис.14.30

В отличие от ранее рассмотренных экви­валентных схем фильтров, содержащих элементы L и С с сосредоточенными пара­метрами, схема рис.14.30 содержит эле­менты (отрезки линий), размеры которых соизмеримы с длиной волны. Такие эле­менты называют элементами с распре­деленными параметрами. Схемы, содер­жащие элементы с распределенными па­раметрами, имеют периодические АЧХ, что связано с периодическими свойствами от­резка линии передачи. Поэтому поведение

схемы рис. 14.30 зависит от соотношения l/L. Например, на частотах, для которых (на рис.14.29), схема ведет себя как ФНЧ; при L/4 < l< L/2 – как ФВЧ; при 0 < l < L/2 - как режекторный фильтр, а при L/4 <l<<ЗL/4 - как ПФ и т.д. Причем если схема рис. 14.30 используется в качестве ПФ, то подобный фильтр будет иметь множество полос пропускания, центры которых находятся на частотах, соответствующих длинам волн в линии и т.д.