Основные понятия и определения

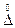В зависимости от характера проявления различают систематическую ( )и случайную ( ) составляющие погрешности измерений, а также грубые погрешности (промахи).

Грубые погрешности (промахи) возникают из-за ошибочных действий оператора, неисправности СИ или резких изменений условий измерений, например, внезапное падение напряжения в сети электропитания. К ним тесно примыкают промахи - погрешности, зависящие от наблюдателя и связанные с неправильным обращением со средствами измерений.

Систематическая погрешность измерения (систематическая погрешность ) – это составляющая погрешности результата измерений, остающаяся постоянной или закономерно изменяющаяся при повторных измерениях одной и той же физической величины.

Считается, что систематические погрешности могут быть обнаружены и исключены. Однако в реальных условиях полностью исключить систематическую составляющую погрешности измерения невозможно. Всегда остаются какие-то факторы, которые нужно учитывать, и которые будут составлять неисключенную систематическую погрешность.

Неисключенная систематическая погрешность (НСП): Составляющая погрешности результата измерений, обусловленная погрешностями вычисления и введения поправок на влияние систематических погрешностей или систематической погрешностью, поправка на действие которой не введена вследствие ее малости.

Неисключенная систематическая погрешность характеризуется её границами.

Границы неисключенной систематической погрешности Θпри числе слагаемых N 3 вычисляют по формуле:

где –граница i–ой составляющей неисключенной систематической погрешности.

При числе неисключенных систематических погрешностей N 4 вычисление проводят по формуле

где К – коэффициент зависимости отдельных неисключенных систематических погрешностей от выбранной доверительной вероятности Р при их

равномерном равномерном распределении (при Р = 0,99, К = 1,4). Здесь Θрассматривается как доверительная квазислучайная погрешность.

Случайная погрешность измерения ( 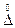) -составляющая погрешности результата измерений, изменяющаяся случайным образом (по знаку и значению) при повторных измерениях, проведенных с одинаковой тщательностью, одной и той же физической величины.

Для уменьшения случайной составляющей погрешности проводят многократные измерения.

Случайная погрешность оценивается доверительным интервалом

где - коэффициент Стьюдента для данного уровня доверительной вероятности Р_д и объема выборки (число измерений) п.

Доверительные границы погрешности результата измерения – границы интервала, внутри которого с заданной вероятностью находится искомое (истинное) значение погрешности результата измерений.

Выборка - ряд из х результатов измерений {х_i}, i=1, ... , п (п>20), из которых исключены известные систематические погрешности. Объем выборки определяется требованиями точности измерений и возможностью производить повторные измерения.

Вариационный ряд – выборка, упорядоченная по возрастанию.

Гистограмма – зависимость относительных частот попадания результатов измерения в интервалы группирования от их значений, представленная в графическом виде.

Оценка закона распределения – оценка соответствия экспериментального закона распределения теоретическому распределению. Проводится с помощью специальных статистических критериев. При п < 15 не проводится.

Точечные оценки закона распределения – оценки закона распределения, полученные в виде одного числа, например, оценка дисперсии результатов измерений или оценка математического ожидания и т.д.

Средняя квадратическая погрешность результатов единичных измерений в ряду измерений (средняя квадратическая погрешность измерений): Оценка рассеяния единичных результатов измерений в ряду равноточных измерений одной и той же физической величины около среднего их значения, вычисляемая по формуле:

где — результат i-го единичного измерения;

— среднее арифметическое значение измеряемой величины из nединичных результатов.

Примечание — На практике широко распространен термин среднее квадратическое отклонение — (СКО). Под отклонением в соответствии с приведенной выше формулой понимают отклонение единичных результатов в ряду измерений от их среднего арифметического значения. В метрологии, это отклонение называется погрешностью измерений.

Средняя квадратическая погрешность результата измерений среднего арифметического: Оценка случайной погрешности среднего арифметического значения результата измерений одной и той же величины в данном ряду измерений, вычисляемая по формуле:

где — средняя квадратическая погрешность результатов единичных измерений, полученная из ряда равноточных измерений;

n — число единичных измерений в ряду.